Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 2 x - 1 ≥ 3 x - m ≤ 0 ⇔ x ≥ 2 x ≤ m . Hệ có nghiệm duy nhất khi và chỉ khi m = 2

x - y = m ( 1 ) x 2 - x y - m - 2 = 0 ( 2 )
Từ (1), ta có y = x - m , thế vào (2) ta được phương trình:
x2 – x (x- m) – m - 2= 0 ⇔ x2 – x2 + mx –m –2 = 0
hay mx –m -2 = 0 (*) .
Hệ phương trình đã cho có nghiệm khi phương trình (*) có nghiệm ⇔ m ≠ 0 .
Chọn B.

a) Xét \(\Delta\) = b2 - 4ac = (-m)2 - 4(2m - 4)
= m2 - 8m + 16 = ( m - 4 )2
Ta có: ( m - 4 )2 \(\ge\) 0
=> Pt luôn có nghiệm
b) Vì phương trình luôn có nghiệm nên áp dụng định lí Ta- lét:
\(\left\{{}\begin{matrix}x_1+x_2=\frac{-b}{a}==m\\x_1x_2=2m-4\end{matrix}\right.\)
Xét phương trình: x12 + x22 - 9
= x12 + x22 + 2x1x2 - 2x1x2 - 9
= (x1 + x2)2 - 2x1x2 - 9
= (-m)2 - 2(2m - 4) - 9
= m2 - 4m + 8 - 9
= m2 - 4m - 1 = m2 - 4m + 4 - 5
= (m - 2)2 - 5
Xét (m - 2)2 \(\ge\) 0
=> (m - 2)2 - 5 \(\ge\) -5
Dấu " =" xảy ra khi m - 2 = 0
<=> m = 2
\(\Delta=m^2-8m+16=\left(m-4\right)^2\ge0\Rightarrow\) pt luôn có nghiệm
Khi đó theo Viet \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=2m-4\end{matrix}\right.\)
\(A=x_1^2+x_2^2-9=\left(x_1+x_2\right)^2-2x_1x_2-9\)
\(A=m^2-2\left(2m-4\right)-9\)
\(A=m^2-4m-1\)
\(A=\left(m-2\right)^2-5\ge-5\)
\(\Rightarrow A_{min}=-5\) khi \(m=-2\)

Pt đã cho có 3 nghiệm pb khi nó có một nghiệm bằng 0
\(\Rightarrow m^2-1=0\Rightarrow m=\pm1\)
- Với \(m=1\Rightarrow-x^2=0\) chỉ có 1 nghiệm (ktm)
- Với \(m=-1\Rightarrow-2x^4+x^2=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\pm\frac{\sqrt{2}}{2}\end{matrix}\right.\) (t/m)
Vậy \(m=-1\)

Ta có \(\Delta'=1-m\ge0\)=>\(m\le1\)
Theo viet ta có
\(x_1+x_2=2\)
Vì x1 là nghiệm của phương trình
=> \(x_1^2=2x_1-m\)
Khi đó
\(P=\frac{m^3-m^2+4m}{2\left(x_1+x_2\right)+m^2-m}+m^2+1\)
\(=\frac{m\left(m^2-m+4\right)}{m^2-m+4}+m^2+1=m^2+m+1=\left(m+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy \(MinP=\frac{3}{4}\)khi \(m=-\frac{1}{2}\)(thỏa mãn \(x\le1\))

Chọn A
TH1. Nếu m+ 3< 0 hay m< - 3.Khi đó :
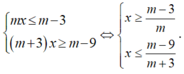
Hệ bất phương trình có nghiệm duy nhất

TH2. Nếu m+3= 0 hay m= -3
Khi đó :
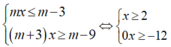
Hay x ≥ -2. Khi đó hệ bpt có vô số nghiệm (loại)
TH3. Nếu m+ 3> 0 hay m> - 3
+ Nếu -3< m< 0
Khi đó :
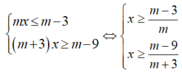
Hệ này có vô số nghiệm ( loại )
+ Nếu m= 0
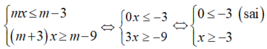
Hệ bất phương trình vô nghiệm( loại)
+ Nếu m> 0
Khi đó :
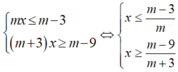
Hệ bất phương trình có nghiệm duy nhất
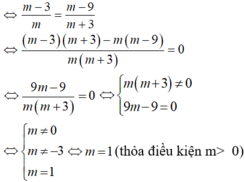
Vậy m= 1 thỏa yêu cầu bài toán.
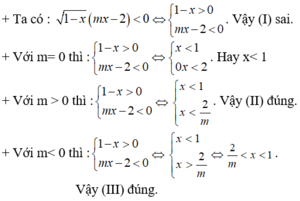
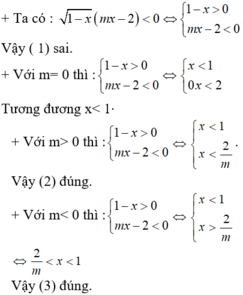
\(\left\{{}\begin{matrix}x+my=m+1\\mx+y=3m-1\end{matrix}\right.\)
Xét \(m=0\) , hệ pt tương đương:
\(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\Rightarrow x+y=0\left(\text{loại}\right)\)
\(\Rightarrow m\ne0\)
Hệ pt có nghiệm duy nhất khi:
\(\frac{1}{m}\ne m\Leftrightarrow m\ne\pm1\)
Hệ pt tương đương:
\(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=3m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+1-my\\y\left(m^2-1\right)=\left(m-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{3m+1}{m+1}\\y=\frac{m-1}{m+1}\end{matrix}\right.\)
\(\Rightarrow x+y=\frac{4m}{m+1}\)
\(x+y< 0\Leftrightarrow\frac{4m}{m+1}< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4m>0\\m+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}4m< 0\\m+1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m>0\\m>-1\end{matrix}\right.\\\left\{{}\begin{matrix}m< 0\\m< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
Vậy để hệ phương trình có nghiệm duy nhất \(\left(x;y\right)\) thỏa mãn \(x+y< 0\) thì \(m>0;m< -1;m\ne1\)