Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Khi $m=1$ thì HPT trở thành:
\(\left\{\begin{matrix} x-2y=-1\\ 2x+y=2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x-4y=-2\\ 2x+y=2\end{matrix}\right.\)
\(\Rightarrow (2x+y)-(2x-4y)=2-(-2)\)
\(\Leftrightarrow 5y=4\Rightarrow y=\frac{4}{5}\)
\(x=\frac{2-y}{2}=\frac{2-\frac{4}{5}}{2}=\frac{3}{5}\)
Vậy ...........
b)
HPT \(\Leftrightarrow \left\{\begin{matrix} mx-2y=m-2\\ y=m+1-2x\end{matrix}\right.\Rightarrow mx-2(m+1-2x)=m-2\)
\(\Leftrightarrow x(m+4)=3m(*)\)
Để HPT ban đầu có bộ nghiệm (x,y) duy nhất thì PT $(*)$ phải có nghiệm $x$ duy nhất. Điều này xảy ra khi $m+4\neq 0$ hay $m\neq -4$
Bài 2:
a)
Khi $m=2$ thì hệ trở thành:
\(\left\{\begin{matrix}
x+2y=1\\
2x+y=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
2x+4y=2\\
2x+y=1\end{matrix}\right.\)
\(\Rightarrow (2x+4y)-(2x+y)=2-1\)
\(\Leftrightarrow 3y=1\Rightarrow y=\frac{1}{3}\)
Khi đó: \(x=1-2y=1-2.\frac{1}{3}=\frac{1}{3}\)
Vậy HPT có bộ nghiệm duy nhất $(x,y)=(\frac{1}{3}, \frac{1}{3})$
b)
HPT \(\Leftrightarrow \left\{\begin{matrix} x=1-my\\ mx+y=1\end{matrix}\right.\Rightarrow m(1-my)+y=1\)
\(\Leftrightarrow y(1-m^2)=1-m(*)\)
Để HPT ban đầu có nghiệm duy nhất thì PT $(*)$ cũng phải có nghiệm duy nhất. Điều này xảy ra khi \(1-m^2\neq 0\Leftrightarrow m\neq \pm 1\)
Khi đó:
\(y=\frac{1-m}{1-m^2}=\frac{1}{1+m}\)
\(x=1-my=1-\frac{m}{m+1}=\frac{1}{m+1}\)
Vậy HPT có nghiệm \((x,y)=(\frac{1}{m+1}, \frac{1}{m+1})\)
Để \(x,y>0\Leftrightarrow \frac{1}{m+1}>0\Leftrightarrow m>-1\)
Kết hợp những điều vừa tìm được suy ra $m>-1$ và $m\neq 1$ thì thỏa mãn.

Khi m = - 1 thì hệ trở thành x + y = 0 x 2 y + y 2 x = 0 ⇒ Hệ có vô số nghiệm => (I) đúng
Ta có: x + y = m + 1 x 2 y + y 2 x = 2 m 2 − m − 3 ⇒ x y m + 1 = 2 m 2 − m − 3
⇒ x y = 2 m − 3
⇒
S
2
−
4
P
=
m
+
1
2
−
4
2
m
−
3
=
m
2
−
6
m
+
13
>
0
,
∀
m
đúng
Đáp án cần chọn là: D

\(\hept{\begin{cases}mx+y=m^2+m+1\\-x+my=m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(my-m^2\right)+y-m^2-m-1=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}\left(m^2y-m^2\right)+\left(y-1\right)-\left(m^3+m\right)=0\\x=my-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m^2+1\right)\left(y-m-1\right)=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}y=m+1\\x=m\left(m+1\right)-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=m\\y=m+1\end{cases}}\)
\(\Rightarrow\)\(x^2+y^2=2m^2+2m+1=2\left(m+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\)
Dấu "=" xảy ra khi \(m=\frac{-1}{2}\) hay hệ có nghiệm \(\left(x;y\right)=\left(\frac{-1}{2};\frac{1}{2}\right)\)

\(\left\{{}\begin{matrix}2x-\left(m^2+m+1\right)y=-m^2-9\left(1\right)\\m^4x+\left(2m^2+1\right)y=1\left(2\right)\end{matrix}\right.\)
rút x từ (1) thế vào (2)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\left(m^2+m+1\right)y-m^2-9}{2}\left(3\right)\\m^4\left[\dfrac{\left(m^2+m+1\right)y-m^2-9}{2}\right]+\left(2m^2+1\right)y=1\left(4\right)\end{matrix}\right.\)
\(\left(4\right)\Leftrightarrow m^4\left(m^2+m+1\right)y-m^4\left(m^2+9\right)+2\left(2m^2+1\right)y=2\)
\(\Leftrightarrow\left[m^4\left(m^2+m+1\right)+4m^2+2\right]y=m^4\left(m^2+9\right)+2\)
\(\Leftrightarrow Ay=B\)
Taco
\(\left\{{}\begin{matrix}m^2+m+1=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\in R\\4m^2+2>0\forall m\in R\\m^4\left(m^2+9\right)>0\forall m\in R\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A>0\forall m\in R\\B>0\forall m\in R\end{matrix}\right.\)
\(\Rightarrow y>0\forall m\in R\)
Kết luận không có m thủa mãn

Ta tính các định thức:
D = m 1 1 m = m 2 - 1 = m + 1 . m - 1 ; D x = m + 1 1 2 m = m 2 + m - 2 = m - 1 . m + 2 ; D y = m m + 1 1 2 = m - 1
Xét D = 0 tức là m = 1 hoặc m = -1.
* Nếu m = 1 thì D = Dx = Dy = 0 nên hệ phương trình đã cho có vô số nghiệm.
Do đó, a= 1.
* Nếu m = -1 thì D = 0 nhưng D x ≠ 0 nên hệ phương trình đã cho vô nghiệm.
Do đó, b = -1
Tổng a+ b = 0.
Chọn A.

a: Khi m=2 thì hệ sẽ là:
2x-y=2 và x+2y=1
=>x=1; y=0
b: \(\left\{{}\begin{matrix}mx-y=2\\x+my=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x=1-my\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x=1-m\left(mx-2\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x=1-m^2x+2m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x\left(1+m^2\right)=2m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{2m^2+m}{m^2+1}-2=\dfrac{-m}{m^2+1}\end{matrix}\right.\)
c: x+y=1 thì \(\dfrac{2m+1}{m^2+1}+\dfrac{-m}{m^2+1}=1\)
=>m^2+1=m+1
=>m=0 hoặc m=-1
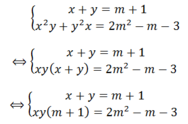


* Ta có: D = m 1 1 m = m 2 - 1 ; D x = m 1 m m = m 2 - m
Để hệ phương trình đã cho vô nghiệm thì:
D = m 2 - 1 = 0 D x = m 2 - m ≠ 0 ⇔ m = ± 1 m ≠ 0 ⇔ m = - 1 m ≠ 1
Vậy hệ vô nghiệm khi m = -1, vậy chọn đáp án là C.