Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm:
\(x^2+2mx-3m=-2x+3\)
\(\Leftrightarrow x^2+2\left(m+1\right)x-3m-3=0\)
Hai đồ thị cắt nhau tại hai điểm phân biệt A, B khi phương trình \(\Leftrightarrow x^2+2\left(m+1\right)x-3m-3=0\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta'=m^2+5m+4>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>-1\\m< -4\end{matrix}\right.\)
Phương trình có hai nghiệm phân biệt \(x=-m-1\pm\sqrt{m^2+5m+4}\)
\(x=-m-1+\sqrt{m^2+5m+4}\Rightarrow y=2m+5-2\sqrt{m^2+5m+4}\)
\(\Rightarrow A\left(-m-1+\sqrt{m^2+5m+4};2m+5-2\sqrt{m^2+5m+4}\right)\)
\(x=-m-1-\sqrt{m^2+5m+4}\Rightarrow y=2m+5+2\sqrt{m^2+5m+4}\)
\(\Rightarrow B\left(-m-1-\sqrt{m^2+5m+4};2m+5+2\sqrt{m^2+5m+4}\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-2\sqrt{m^2+5m+4};4\sqrt{m^2+5m+4}\right)\)
\(\Rightarrow AB=\sqrt{4\left(m^2+5m+4\right)+16\left(m^2+5m+4\right)}=2\sqrt{5\left(m^2+5m+4\right)}=4\sqrt{5}\)
\(\Leftrightarrow\sqrt{m^2+5m+4}=2\)
\(\Leftrightarrow m^2+5m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=-5\left(tm\right)\end{matrix}\right.\)
Xét phương trình hoành độ giao điểm của (d): y = -2x + 3 và
(P) : x2 + 2mx - 3m = 0
x2 + 2mx - 3m = -2x + 3
⇔ x2 + 2(m+1) - 3(m+1) = 0 (*)
Để (d) cắt (P) taị 2 điểm phân biệt thì (*) có hai nghiệm phân biệt. Khi đó Δ' > 0
⇔ (m+1)2 + 3(m+1) > 0
⇔ (m+1)(m+4) > 0
⇔ m ∈ R \ (-4 ; -1) (!)
Do A,B là giao điểm của (d) và (P) nên hoành độ của chúng là nghiệm của (*)
Theo định lí Viet : \(\left\{{}\begin{matrix}x_A+x_B=-2m-2=-2\left(m+1\right)\\x_A.x_B=-3m-3=-3\left(m+1\right)\end{matrix}\right.\)
Do A,B ∈ d nên hoành độ và tung độ của chúng thỏa mãn
y = -2x + 3 hay \(\left\{{}\begin{matrix}y_A=-2x_A+3\\y_B=-2x_B+3\end{matrix}\right.\)
Để giải được bài này thì mình sẽ sử dụng công thức tính độ dài của vecto AB (nếu bạn chưa học đến thì xin lỗi)
AB = |\(\overrightarrow{AB}\)| = 4\(\sqrt{5}\)
⇒ (xA - xB)2 + (yA - yB)2 = 80
⇒ (xA - xB)2 + (-2xA + 2xB)2 = 80
Sau đó bạn thay m vào rồi biến đổi, kết quả ta được
(m+1)(m+4) = 4 \(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-5\end{matrix}\right.\)(thỏa mãn (!) )
Vậy tập hợp các giá trị của m thỏa mãn yêu cầu bài toán là
M = {0 ; -5}

Lời giải:
Để 2 ĐTHS cắt nhau tại 2 điểm phân biệt $A,B$ thì PT hoành độ giao điểm: $x^2+2mx-3m=-2x+3\Leftrightarrow x^2+2x(m+1)-(3m+3)=0$ có 2 nghiệm phân biệt $x_A,x_B$
Điều này xảy ra khi:
$\Delta'=(m+1)^2+(3m+3)>0$
$\Leftrightarrow (m+1)(m+4)>0\Leftrightarrow m>-1$ hoặc $m< -4$
Áp dụng định lý Vi-et: \(\left\{\begin{matrix} x_A+x_B=-2(m+1)\\ x_Ax_B=-3(m+1)\end{matrix}\right.\)
Khi đó:
\(AB=4\sqrt{5}\)
\(\Leftrightarrow AB^2=80\)
\(\Leftrightarrow (x_A-x_B)^2+(y_A-y_B)^2=80\)
\(\Leftrightarrow (x_A-x_B)^2+[(-2x_A+3)-(-2x_B+3)]^2=80\)
\(\Leftrightarrow 5(x_A-x_B)^2=80\)
\(\Leftrightarrow (x_A-x_B)^2=16\Leftrightarrow (x_A+x_B)^2-4x_Ax_B=16\)
\(\Leftrightarrow 4(m+1)^2+12(m+1)=16\)
\\(\Leftrightarrow (m+1)^2+3(m+1)-4=0\)
\(\Leftrightarrow (m+1-1)(m+1+4)=0\)
$\Leftrightarrow m=0$ hoặc $m=-5$ (đều thỏa mãn)

Phương trình hoành độ giao điểm: x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0
(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4
Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2
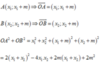
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4
Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2 khi m = − 5 2
Đáp án cần chọn là: A
Bạn tham khảo lời giải tại đây:
Câu hỏi của Lê Quynh Nga - Toán lớp 10 | Học trực tuyến