Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)

Hoành độ giao điểm của d : y = mx+2 với (C) là nghiệm phương trình :
\(\begin{cases}x>0\\\log^2_2x-\log_2x^2-3\ge0\end{cases}\)
Dễ thấy với m = 0 thì (1) vô nghiệm. Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt khác -1. Điều kiện là
\(\begin{cases}\Delta>0\\m\left(-1\right)^2+m\left(-1\right)+3\ne0\end{cases}\) \(\Leftrightarrow m^2-12m>0\) \(\Leftrightarrow m<0\) hoặc m > 12 (*)
Với (*) giả sử x1, x2 là 2 nghiệm phân biệt của (1), khi đó tọa độ các giao điểm là :
\(A\left(x_1;mx_1+2\right);B\left(x_2;mx_2+2\right)\)
Dễ thất điểm O không thuộc d nên ABO là một tam giác.
Tam giác ABO vuông tại O khi và chỉ khi :
\(\overrightarrow{OA}.\overrightarrow{OB}=0\Leftrightarrow\left(1+m^2\right)x_1x_2+2m\left(x_1+x_2\right)+4=0\)
Áp dụng định lí Viet ta có : \(x_1+x_2=-1;x_1x_2=\frac{3}{m}\)
Thay vào trên ta được :
\(m^2+4m+3=0\Leftrightarrow m=-3\) hoặc \(m=-1\) (thỏa mãn (*)
Vậy \(m=-3\) hoặc \(m=-1\)

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
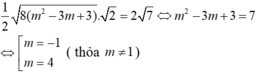
Chọn B.

Phương pháp:
+) Tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Sử dụng công thức tính diện tích tam giác
![]()
+) Sử dụng công thức tính độ dài ![]()
+) Áp dụng định lí Vi-ét tìm m
Chọn C.

Phương trình có hoành độ giao điểm \(\frac{-x+m}{x+2}=-x+\frac{1}{2}\Leftrightarrow\begin{cases}x\ne-2\\2x^2+x+2m-2=0\left(1\right)\end{cases}\)
Đường thẳng (d) cắt \(\left(C_m\right)\) tại 2 điểm A, B <=> (1) có 2 nghiệm phân biệt \(x\ne-2\)
\(\Leftrightarrow\begin{cases}\Delta=1-8\left(2m-2\right)>0\\2\left(-2\right)^2+\left(-2\right)+2m-2\ne0\end{cases}\)\(\Leftrightarrow\begin{cases}17-16m>0\\m\ne-2\end{cases}\)\(\Leftrightarrow\begin{cases}m<\frac{17}{16}\\m\ne-2\end{cases}\)
\(A\left(x_1;-x_1+\frac{1}{2}\right);B\left(x_2;-x_2+\frac{1}{2}\right);\) trong đó x1, x2 là 2 nghiệm phân biệt của phương trình (1)
Theo Viet ta có \(\begin{cases}x_1+x_2=-\frac{1}{2}\\x_1x_2=m-1\end{cases}\)
\(AB=\sqrt{\left(x_2-x_1\right)^2+\left(x_1-x_2\right)^2}=\sqrt{2\left[\left(x_1+x_2\right)^2-4x_1x_2\right]}=\frac{\sqrt{2\left(17-16m\right)}}{2}\)
\(d\left(O,d\right)=\frac{1}{2\sqrt{2}};S_{\Delta OAB}=\frac{1}{2}AB.d\left(O,d\right)=\frac{1}{2}.\frac{1}{2\sqrt{2}}.\frac{\sqrt{2\left(17-16m\right)}}{2}=1\)
\(\Leftrightarrow m=\frac{-47}{16}\)
Vậy \(m=\frac{-47}{16}\)

Lời giải:
PT hoành độ giao điểm:
\(x^2(m-1)+x(12-7m)+(10m-29)=0(1)\)
Để hai đồ thị hàm số cắt nhau tại hai điểm phân biệt thì PT $(1)$ phải có hai nghiệm phân biệt \(\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ \Delta=(12-7m)^2-4(m-1)(10m-29)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ 9m^2-12m+28=(3m-2)^2+24>0\end{matrix}\right.\Leftrightarrow m\neq 1\)
Khi đó , áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của $(1)$ thì: \(x_1+x_2=\frac{7m-12}{m-1}\)
Hai giao điểm của hai ĐTHS là \(A(x_1,m(x_1-5)+10);B(x_2,m(x_2-5)+10)\)
\(M(5,10)\) là trung điểm của $AB$
\(\Leftrightarrow \left\{\begin{matrix} \frac{x_1+x_2}{2}=5\\ \frac{y_1+y_2}{2}=\frac{m(x_1+x_2)-10m+20}{2}=10\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{7m-12}{m-1}=10\\ \frac{m(7m-12)}{m-1}=10m\end{matrix}\right.\)
Suy ra \(m=\frac{-2}{3}\) (thỏa mãn)

Lời giải:
PT hoành độ giao điểm:
\(x+m-\frac{2x-1}{x-1}=0\Leftrightarrow x^2+x(m-3)+(1-m)=0\) \((1)\)
Để hai ĐTHS cắt nhau ở hai điểm thì PT $(1)$ phải có hai nghiệm phân biệt \(\Leftrightarrow \Delta=(m-3)^2-4(1-m)>0\Leftrightarrow (m-1)^2+4>0\)
(luôn đúng với mọi $m$ )
Khi đó với \(x_1,x_2\) là hai nghiệm của PT trên thì \(A(x_1,x_1+m) ; B(x_2,x_2+m)\) là hai giao điểm của 2 ĐTHS.
Không mất tổng quát, giả sử tam giác $OAB$ vuông tại $A$
\(\Rightarrow \overrightarrow{OA}\perp \overrightarrow{AB}\Leftrightarrow (x_1,x_1+m)\perp (x_2-x_1,x_2-x_1)\)
\(\Leftrightarrow x_1(x_2-x_1)+(x_2-x_1)(x_1+m)=0\)
\(\Rightarrow 2x_1+m=0\Rightarrow x_1=\frac{-m}{2}\)
Mà áp dụng định Viete: \(\left\{\begin{matrix} x_1+x_2=3-m\\ x_1x_2=1-m\end{matrix}\right.\Rightarrow x_1=3-m-x_1=\frac{1-m}{x_1}\)
\(\Leftrightarrow 3-\frac{m}{2}=\frac{2(m-1)}{m}\Rightarrow m=1\pm \sqrt{5}\) (thỏa mãn )
Vậy \(m=1\pm \sqrt{5}\)


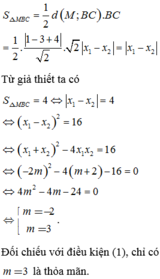
Lời giải:
PT hoành độ giao điểm:
\(m-\frac{-x^2+2x-4}{x-2}=0\Leftrightarrow x^2+x(m-2)+(4-2m)=0\)
Để 2 ĐTHS cắt nhau tại hai điểm phân biệt thì PT trên phải có hai nghiệm phân biệt
\(\Leftrightarrow \Delta (m-2)^2-4(4-2m)>0\Leftrightarrow m^2+4m-12>0\)
\(\Leftrightarrow \) \(\left[{}\begin{matrix}m< -6\\m>2\end{matrix}\right.\)
Khi đó, với $x_1,x_2$ là hai nghiệm của PT, áp dụng định lý Viete:
\(\left\{\begin{matrix} x_1+x_2=2-m\\ x_1x_2=4-2m\end{matrix}\right.\)
Hai giao điểm là \(A(x_1,m);B(x_2,m)\)
\(\Rightarrow AB=\sqrt{(x_1-x_2)^2}=\sqrt{m^2+4m-12}\)
Mặt khác \(d(O,AB)=|m|\)
\(\Rightarrow S_{OAB}=\frac{d(O,AB).AB}{2}=3\Leftrightarrow |m|\sqrt{m^2+4m-12}=6\)
\(\Rightarrow m\approx -6,11845\) hoặc \(m\approx 2,61246\) (đều thỏa mãn)