Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m

Dạng: \(....f'\left(x\right)+...f\left(x\right)=...\)
Ý tưởng luôn là đưa về đạo hàm của tổng sau đó lấy nguyên hàm 2 vế.
Thêm bớt sao cho vế trái biến thành: \(u\left(x\right).f'\left(x\right)+u'\left(x\right).f\left(x\right)\) là được
So sánh nó với vế trái đề bài, dư ra \(u'\left(x\right)\) ở trước \(f\left(x\right)\) nên ta chia nó (vế kia vẫn ko quan tâm)
Được: \(\dfrac{u\left(x\right)}{u'\left(x\right)}.f'\left(x\right)+f\left(x\right)\)
So sánh nó với đề bài, vậy ta cần tìm hàm \(u\left(x\right)\) sao cho:
\(\dfrac{u\left(x\right)}{u'\left(x\right)}=x\left(x+1\right)\)
Nhưng để thế này ko lấy nguyên hàm được, phải nghịch đảo 2 vế:
\(\dfrac{u'\left(x\right)}{u\left(x\right)}=\dfrac{1}{x\left(x+1\right)}\)
Giờ thì lấy nguyên hàm: \(\int\dfrac{u'\left(x\right)}{u\left(x\right)}dx=\int\dfrac{dx}{x\left(x+1\right)}\Leftrightarrow ln\left|u\left(x\right)\right|=ln\left|\dfrac{x}{x+1}\right|+C\)
Tới đây suy được \(u\left(x\right)=\dfrac{x}{x+1}\) \(\Rightarrow\) vế trái cần có dạng:
\(\dfrac{x}{x+1}f'\left(x\right)+\dfrac{1}{\left(x+1\right)^2}f\left(x\right)\)
Nhìn vào đây là xong rồi. Bài toán sẽ được giải như sau:
Chia 2 vế giả thiết cho \(\left(x+1\right)^2\):
\(\Rightarrow\dfrac{x}{x+1}f'\left(x\right)+\dfrac{1}{\left(x+1\right)^2}f\left(x\right)=\dfrac{x}{x+1}\)
\(\Leftrightarrow\left(\dfrac{x}{x+1}+f\left(x\right)\right)'=\dfrac{x}{x+1}\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\dfrac{x}{x+1}+f\left(x\right)=\int\dfrac{x}{x+1}dx=\int\left(1-\dfrac{1}{x+1}\right)dx=x-ln\left|x+1\right|+C\)
\(\Rightarrow f\left(x\right)=x-\dfrac{x}{x+1}-ln\left|x+1\right|+C=\dfrac{x^2}{x+1}-ln\left|x+1\right|+C\)
Thay \(x=1\)
\(\Rightarrow f\left(1\right)=\dfrac{1}{2}-ln2+C\Rightarrow-2ln2=\dfrac{1}{2}-ln2+C\)
\(\Rightarrow C=-ln2-\dfrac{1}{2}\)
\(\Rightarrow f\left(x\right)=\dfrac{x^2}{x+1}-ln\left|x+1\right|-ln2-\dfrac{1}{2}\)
\(\Rightarrow f\left(2\right)=...\)

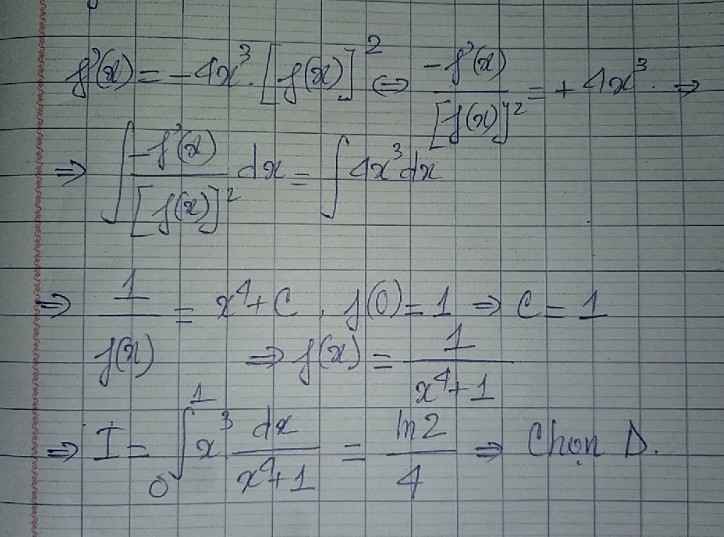


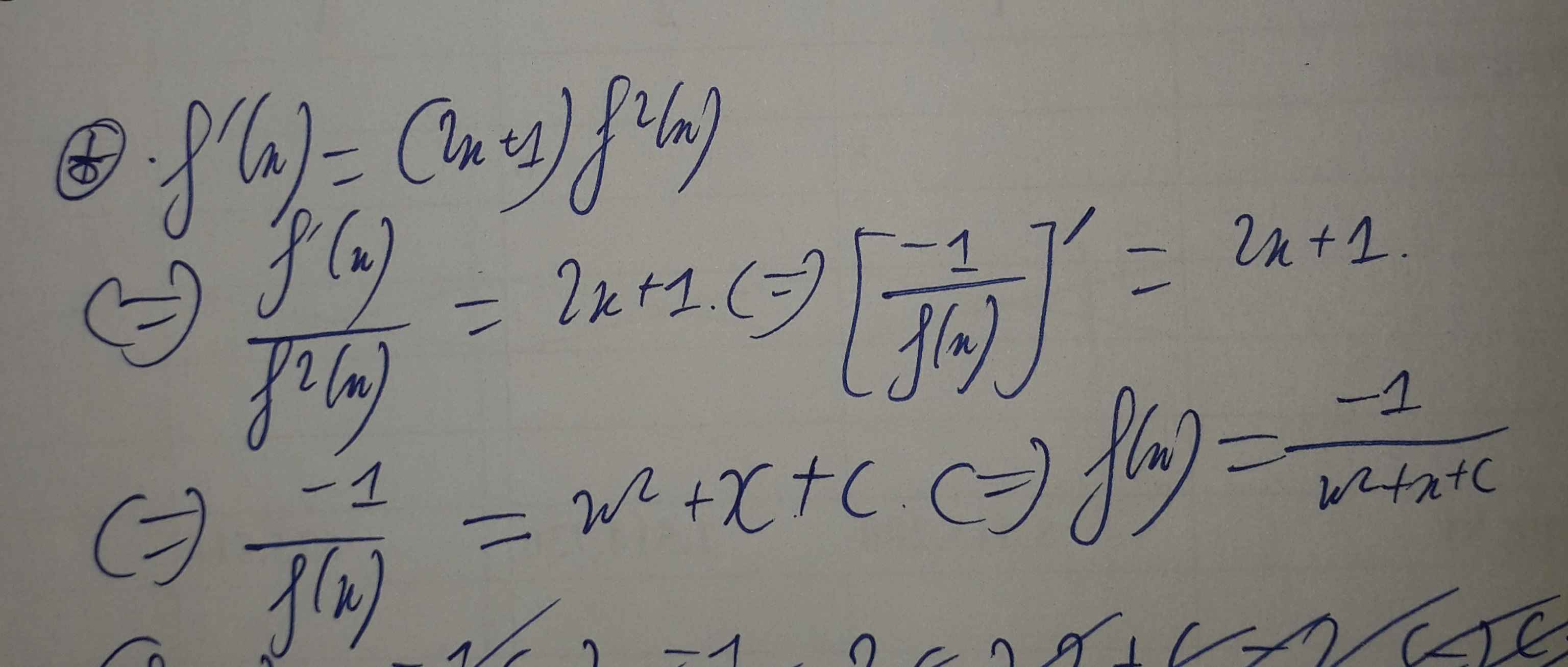
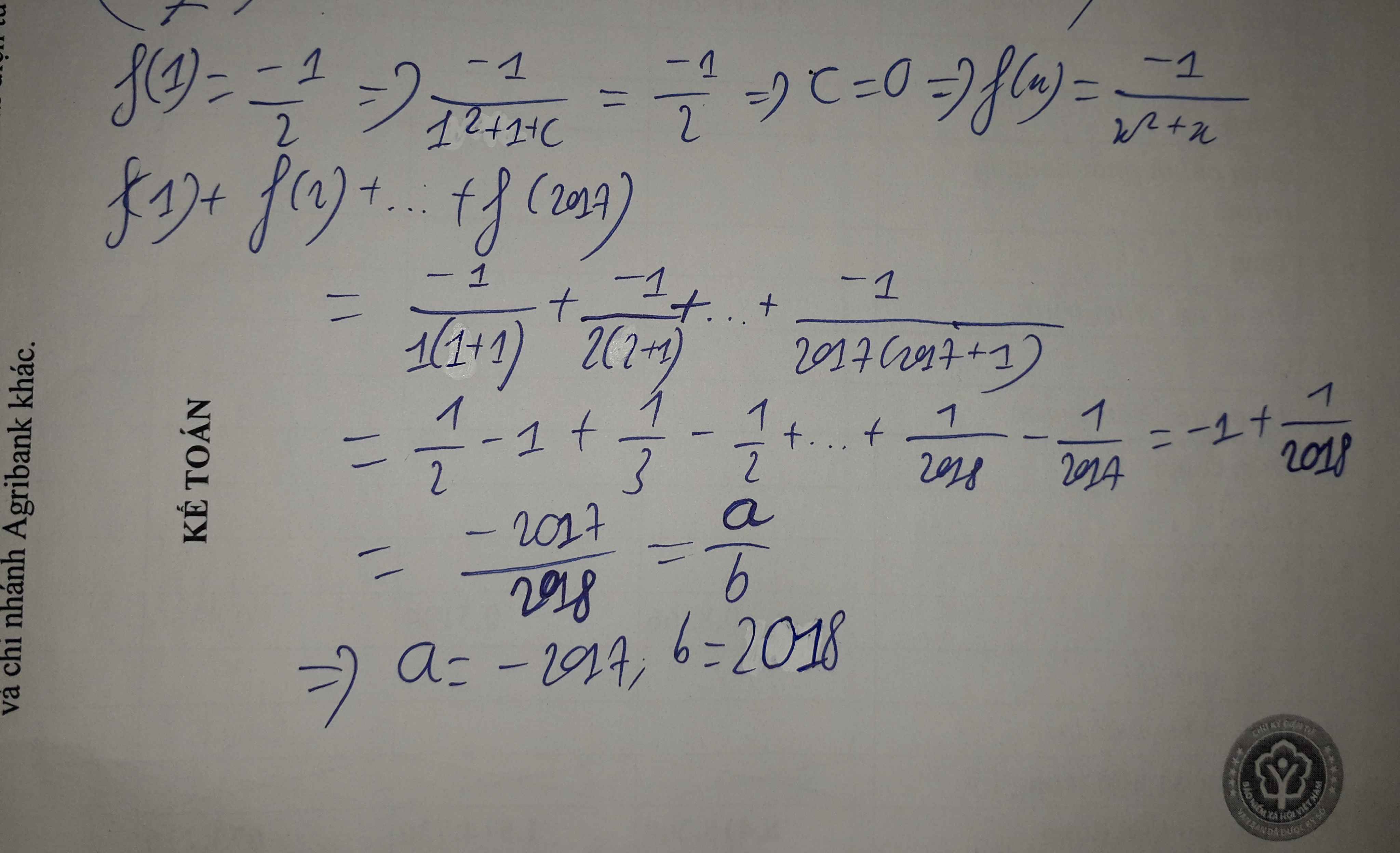
\(f'\left(x\right)=-e^x.f^2\left(x\right)\Leftrightarrow\frac{f'\left(x\right)}{f^2\left(x\right)}=-e^x\)
Lấy nguyên hàm 2 vế:
\(\int\frac{f'\left(x\right)}{f^2\left(x\right)}dx=-\int e^xdx\)
\(\Rightarrow-\frac{1}{f\left(x\right)}=-e^x-C\)
\(\Rightarrow f\left(x\right)=\frac{1}{e^x+C}\)
\(f\left(0\right)=\frac{1}{2}\Rightarrow\frac{1}{1+C}=\frac{1}{2}\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\frac{1}{e^x+1}\Rightarrow f\left(ln2\right)=\frac{1}{e^{ln2}+1}=\frac{1}{3}\)