Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=-1 và y=3 vào y=ax, ta được:
-a=3
hay a=-3

a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3

a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2

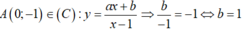
- Ta có: 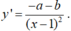
- Hệ số góc của tiếp tuyến với đồ thị tại điểm A là: k = y'(0)
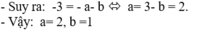
Chọn B.

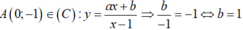
- Ta có: 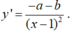
- Hệ số góc của tiếp tuyến với đồ thị tại điểm A là: k = y'(0)
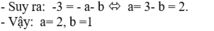
Chọn B.

Đáp án D.
- Ta có: 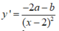
+) Giao điểm của tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox là 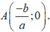
+ ) Tiếp tuyến tại A có phương trình: 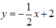
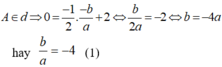
+) Tiếp tuyến tại A có hệ số góc 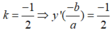
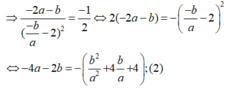
- Giải hệ phương trình (1) và (2) ta được: a = -1, b = 4.
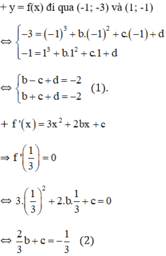

\(A\left(1;3\right)\) thuộc đths \(\Rightarrow a+b+c+1=3\Rightarrow a+b+c=2\) (1)
\(B\left(-1;4\right)\) thuộc đths \(\Rightarrow-a+b-c+1=4\Rightarrow-a+b-c=3\) (2)
Ta có \(y'\left(x\right)=3ax^2+2bx+c\)
\(y'\left(2\right)=0\Rightarrow12a+4b+c=0\) (3)
Từ (1), (2) và (3) ta được \(a=-\dfrac{19}{22};b=\dfrac{5}{2};c=\dfrac{4}{11}\)
Vậy hàm số đã cho là \(y=-\dfrac{19}{22}x^3+\dfrac{5}{2}x^2+\dfrac{4}{11}x+1\)