

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)

\(g\left(x\right)=3x^4-4x^3-6mx^2+12mx\)
\(g'\left(x\right)=12x^3-12x^2-12mx+12m=0\)
\(\Leftrightarrow12x^2\left(x-1\right)-12m\left(x-1\right)=0\)
\(\Leftrightarrow12\left(x^2-m\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x^2=m\end{matrix}\right.\)
Xét \(g\left(x\right)=0\Leftrightarrow x\left(3x^3-4x^2-6mx+12m\right)=0\)
- Nếu \(m=0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ \(\Rightarrow f\left(x\right)\) có 3 cực trị (thỏa mãn)
- Nếu \(m=\dfrac{1}{6}\Rightarrow g'\left(x\right)=0\) có 3 nghiệm bội lẻ, \(g\left(x\right)=0\) có 3 nghiệm pb nhưng chỉ có 1 nghiệm \(x=1\) trùng với \(g'\left(x\right)=0\) nên hàm có 5 cực trị (ktm)
- Nếu \(m=1\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (thỏa mãn)
- Nếu \(m< 0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ \(x=1\)
Khi đó hàm có 3 cực trị khi \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (hiển nhiên từ các TH này thì \(g\left(x\right)=0\) ko thể có nghiệm \(x=1\) do đã loại trừ từ TH \(m=\dfrac{1}{6}\))
\(\Leftrightarrow3x^3-4x^2-6mx+12m=0\) có đúng 1 nghiệm
\(\Leftrightarrow3x^3-4x^2=6m\left(x-2\right)\Leftrightarrow m=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) (do \(x=2\) ko là nghiệm)
Khảo sat \(h\left(x\right)=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) ta được \(y=m\) cắt \(y=h\left(x\right)\) tại đúng 1 điểm khi: \(\left[{}\begin{matrix}m< 0\\\dfrac{1}{6}< m< \dfrac{64}{9}\\\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
- Nếu \(m>0;m\ne\left\{\dfrac{1}{6};1\right\}\) \(\Rightarrow g'\left(x\right)=0\) có 3 nghiệm pb
Mà \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm bội lẻ \(x=0\)
\(\Rightarrow\) Hàm có 3 cực trị khi và chỉ khi:
TH1: \(3x^3-4x^2-6mx+12m=0\) vô nghiệm (vô lý do hàm bậc 3 luôn có nghiệm)
Th2: \(3x^3-4x^2-6mx+12m=0\) (1) có 3 nghiệm đều trùng với nghiệm của \(g'\left(x\right)=0\) (vô lý do \(m\ne\dfrac{1}{6}\) nên nếu (1) có nghiệm thì nó luôn có nghiệm khác 1)
Kết luận: \(\left[{}\begin{matrix}m=1\\m\le0\end{matrix}\right.\)
lúc đầu mk giải câu này theo kiểu xét 3 trường hợp là m < 0; 1 nằm giữa hai nghiệm kia; 1 nằm bên phải 2 nghiệm kia. Không biêt cách này có đúng không mà tính ra kết quả là 10 giá trị ???

Ta có
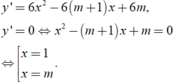
Để hàm số có hai điểm cực trị khi m khác -1
Tọa độ các điểm cực trị là A( 1; m3+ 3m-1) và B( m; 3m2)
Suy ra
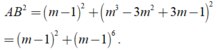
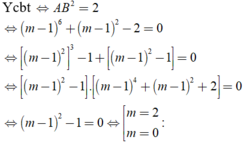
Chọn B.

\(y'=6x^2-6\left(m+1\right)x+6m\)
\(y'=0\Leftrightarrow x^2-\left(m+1\right)x+m=0\)
\(a+b+c=0\Rightarrow\left\{{}\begin{matrix}x=1\\x=m\end{matrix}\right.\)
\(\Rightarrow1^2+m^2=2\Rightarrow m=\pm1\)
Có 2 giá trị m nguyên thỏa mãn

\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?

Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
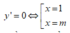
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
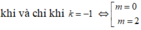

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
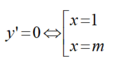
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 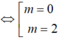
Chọn C.