Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
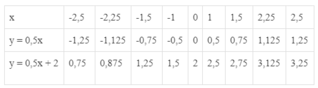
b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.

Thay \(y=a-x\) vào biểu thức \(P\).Vì \(x+y=a\); \(x,y\ge0\); \(0\le x,y\le a\)
Ta có : \(P=40x+x\left(a-x\right)=-x^2+\left(40+a\right)x\)
Nếu \(a\ge40\):
\(P=-\left[x^2+\left(40+a\right)x\right]\)
\(P=\left(\frac{40+a}{2}\right)^2-\left[x^2-2x\cdot\frac{40+a}{2}+\left(\frac{40+a}{2}\right)^2\right]\)
\(P=\left(\frac{40+a}{2}\right)^2-\left(x-\frac{40+a}{2}\right)^2\)
Dễ thấy \(\left(x-\frac{40+a}{2}\right)^2\ge0\)với mọi \(0\le x\le a\)
\(\Leftrightarrow P\le\left(\frac{40+a}{2}\right)^2\)
Dấu " = " xảy ra khi và chỉ khi \(\hept{\begin{cases}x=\frac{40+a}{2}\\b=\frac{a-40}{2}\end{cases}}\)
Nếu \(a< 40\)
\(P=-x^2+\left(40+a\right)x\)
\(P=40x-ax+a^2-\left(x-a\right)^2a\)
\(P=x\left(40-a\right)+a^2-\left(x-a\right)^2\)
Vì \(a< 40\); \(x\le a\)
\(\Rightarrow x\left(40-a\right)\le a\left(40-a\right)\)
\(\left(x-a\right)^2\ge0\)với mọi \(0\le x\le a\)
Do đó : \(P\le a\left(40-a\right)+a^2=40a\)
Dấu " = " xảy ra : \(\hept{\begin{cases}x=a\\y=0\end{cases}}\)
Vậy ....
Nguồn : h.o.c.24

* Hàm số y = 2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y giảm
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y tăng
* Hàm số y = -2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y tăng
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y giảm

* Hàm số y = 2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y giảm
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y tăng
* Hàm số y = -2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y tăng
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y giảm

a) Để hàm số y = (2m - 3)x - 1 // với đường thẳng y = -5x + 3
<=> \(\hept{\begin{cases}2m-3=-5\\-1\ne3\end{cases}}\)<=> 2m = -2 <=> m = -1
b) Hàm số y = (2m - 3)x - 1 đi qua điểm A(-1; 0) => x = -1 và y = 0
Do đó: 0 = (2m - 3).(-1) - 1 = 0 <=> 3 - 2m = 1 <=> 2m = 2 <=> m = 1
Vậy để đò thị hàm số đi qua A(-1; 0) <=> m = 0
c) Gọi tọa độ gđ của 3 đường thẳng y = (2m- 3 )x - 1 , y = 1 và y = 2x - 5 là (x0; y0)
Do đó: \(\hept{\begin{cases}y_0=\left(2m-3\right)x_0-1\\y_0=1\\y_0=2x_0-5\end{cases}}\) <=> \(\hept{\begin{cases}1=\left(2m-3\right)x_0-1\\2x_0-5=1\end{cases}}\)
<=> \(\hept{\begin{cases}\left(2m-3\right)x_0=2\\2x_0=6\end{cases}}\) <=> \(\hept{\begin{cases}\left(2m-3\right).3=2\\x_0=3\end{cases}}\) <=> 2m - 3 = 2/3 <=> 2m = 11/3 <=> m = 11/6
Vậy m = 11/6 thì đồ thị hàm số đã cho và các đường thẳng y = 0 và y = 2x - 5 đồng quy tại 1 điểm

Các giá trị của y được thể hiện trong bảng sau:
| x | 0 | 1 | 2 | 3 + 2 | 3 - 2 |
| y = (3 - 2 )x + 1 | 1 | 4 - 2 | 3 2 - 1 | 8 | 12 - 6 2 |
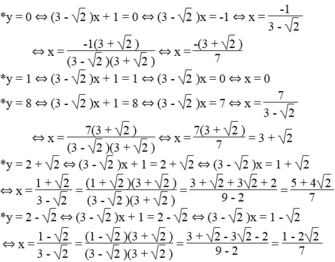
a) Để y nhận giá trị âm điều kiện là : 3x - 1 < 0 ↔ 3x < 1 ↔ x < \(\frac{1}{3}\)
Vậy với x < \(\frac{1}{3}\) thì y nhận giá trị âm
b) Để y nhận giá trị lớn hơn 5 điều kiện là : 3x - 1 > 5 ↔ 3x > 6 ↔ x > 2
Vậy với x > 2 thì y nhận giá trị lớn hơn 5
thích chơi trò mèo đuổi chuột à