Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
đây là dạng toán viết phương trình tiếp tuyến tại một điểm A(a,b)
ta là như sau:
bước 1: tính y'
bước 2: tính y'(a)
bước 3: áp dụng công thức y=y'(a)(x-a)+b
áp dụng vào bài trên ta có
\(y'=3x^2-3\)
\(y'\left(0\right)=-3\)
vậy phương trình tiếp tuyến của đồ thị có dạng
\(y=-3\left(x-0\right)+\left(-1\right)=-3x-1\)
Gọi 
là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
Theo giả thiết, ta có 
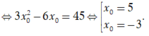
Với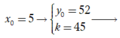 
Phương trình tiếp tuyến: y = 45x - 173
Đáp án A
Ta có y ' = − 3 x − 1 2
Do tiếp tuyến vuông góc với đường thẳng y = 1 3 x − 5 nên − 3 x 0 − 1 2 . 1 3 = − 1 ⇔ x 0 = 2 x 0 = 0
Do tiếp điểm có hoành độ dương nên x 0 = 2 ⇒ P T T T : y = − 3 x − 2 + 4 = − 3 x + 10
Đáp án B
Phương trình tiếp tuyến tại x 0 ; y 0 có hệ số góc là k = y ' = − 3 x − 1 2
Để tiếp tuyến tại x 0 ; y 0 song song với đường thẳng d : y = − 3 x − 1 thì
k = − 3 x − 1 2 = − 3 ⇔ x − 1 2 = 1 ⇔ x 1 = 2 x 2 = 0 ⇔ y 1 = 5 y 2 = − 1 ⇔ d 1 : y = − 3 x + 11 d 2 : y = − 3 x − 1 ≡ d ( l o a i )
Gọi 
là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
Theo giả thiết, ta có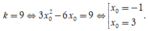 
Với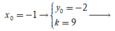 
Phương trình tiếp tuyến cần tìm là: y = 9x + 7 (loại)(vì trùng với đường thẳng đã cho).
Với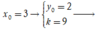 
Phương trình tiếp tuyến cần tìm là: y = 9x - 25
Chọn B.
ta tính \(y'=3x^2\)
để tiếp tuyến của đồ thị hàm số song song với đường thẳng \(y=-3x+1\) thì \(y'\left(x_0\right)=\frac{-1}{-3}=\frac{1}{3}\) giả pt suy ra đc \(x_0=\pm\frac{1}{3}\)
TH1: \(x_0=\frac{1}{3}\) suy ra \(y_0=\frac{1}{27}+1=\frac{28}{27}\)
vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x-\frac{1}{3}\right)+\frac{28}{27}=\frac{1}{3}x+\frac{25}{27}\)
TH2:\(x_0=-\frac{1}{3}\) suy ra \(y_0=-\frac{1}{27}+1=\frac{26}{27}\)
vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x+\frac{1}{3}\right)+\frac{26}{27}=\frac{1}{3}x+\frac{29}{27}\)