Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y'=1/3*3x^2-2x+3=x^2-2x+3=(x-1)^2+2>0
=>y=1/3x^3-x^2+3x+4 luôn đồng biến trên từng khoảng xác định
\(y=\sqrt{x^2+4}\)
=>\(y'=\dfrac{-\left(x^2+4\right)'}{\left(x^2+4\right)^2}=\dfrac{-\left(2x\right)}{\left(x^2+4\right)^2}\)
=>Hàm số này không đồng biến trên từng khoảng xác định
\(y=x^3+4x-sinx\)
=>y'=3x^2+4-cosx
-1<=-cosx<=1
=>3<=-cosx+4<=5
=>y'>0
=>Hàm số luôn đồng biến trên từng khoảng xác định
y=x^4+x^2+2
=>y'=4x^3+2x=2x(2x^2+1)
=>Hàm số ko đồng biến trên từng khoảng xác định

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Ta có \(y'=-2x^2+2\left(m+1\right)x+2m\)
Hàm số đồng biến trên khoảng (0;2) \(\Leftrightarrow y'\ge0,x\in\left(0;2\right)\) (*)
Vì y'(x) liên tục tại x=0 và x=2 nên (*) \(\Leftrightarrow y'\ge0,x\in\left[0;2\right]\)
\(\Leftrightarrow-2x^2+2\left(m+1\right)x+2m\ge0,x\in\left[0;2\right]\)
\(\Leftrightarrow m\left(x+1\right)\ge x^2-x,x\in\left[0;2\right]\Leftrightarrow m\ge g\left(x\right),x\in\left[0;2\right]\); (trong đó \(g\left(x\right)=\frac{x^2-x}{x+1}\))
\(\Leftrightarrow m\ge Max_{\left[0;2\right]}g\left(x\right)\)
Xét hàm số \(g\left(x\right)=\frac{x^2-x}{x+1}\) trên đoạn \(\left[0;2\right]\)
\(\Rightarrow g'\left(x\right)=\frac{x^2+2x-1}{\left(x+1\right)^2}\Rightarrow g'\left(x\right)=0\Leftrightarrow x=-1+\sqrt{2},x\in\left[0;2\right]\)
\(g\left(0\right);g\left(2\right)=\frac{2}{3};g\left(-1+\sqrt{2}\right)\Rightarrow Max_{\left(0;+\infty\right)}g\left(x\right)=\frac{2}{3}\) tại x=2
Vậy \(m\ge\frac{2}{3}\) thì hàm số đồng biến trên khoảng (0;2)
Ta có : \(y'=-2x^2+2\left(m+1\right)x+2m,\Delta'=m^2+6m+1\)
Suy ra hàm đồng biến trên khoảng (0; 2) \(\Leftrightarrow y'\ge0,x\in\left(0;2\right)\)(*)
Trường hợp 1 : Nếu \(\Delta'\le0\Leftrightarrow m^2+6m+1\le0\Leftrightarrow-3-2\sqrt{2}\le m\le-3+2\sqrt{2}\)
theo định lí về dấu tam thức bậc 2 ta có \(y'\le0,x\in R\) => (*) không thỏa mãn
Trường hợp 2 : Nếu \(\Delta'>0\Leftrightarrow m^2+6m+1>0\Leftrightarrow m\le-3-2\sqrt{2}\) hoặc \(m\ge-3+2\sqrt{2}\) thì (*) đúng
<=> phương trình \(y'=0\) có 2 nghiệm phân biệt \(x_1;x_2\) (\(x_1\)>\(x_2\)) và thỏa mãn \(x_1\le0<2\le x_2\)
\(\Leftrightarrow\begin{cases}\Delta>0\\x_1\le0<2\le x_2\end{cases}\) \(\Leftrightarrow\begin{cases}\left(x_1-2\right)\left(x_2-2\right)\le0\\\Delta>0\\\left(x_1-0\right)\left(x_2-0\right)\le0\end{cases}\)
\(\Leftrightarrow\begin{cases}x_1x_2-2\left(x_1+x_2\right)+4\le0\\\Delta>0\\x_1x_2\le0\end{cases}\)
\(\Leftrightarrow m\ge\frac{2}{3}\)
Kết hợp trường hợp 1 và trường hợp 2 ta có \(m\ge\frac{2}{3}\) thì hàm đồng biến trên khoảng (0;2)

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

Ta có \(y'=-\left(m-1\right)x^2+2\left(m+2\right)+3m\) \(\Rightarrow\) Hàm đồng biến trên khoảng \(\left(-\infty;-2\right)\Leftrightarrow y'\ge0,x\in\left(-\infty;-2\right)\)(*)
Vì y'(x) liên tục tại x = -2 nên (*) \(\Leftrightarrow y'\ge0;\)
và mọi x thuộc (-\(-\infty;2\) ] (*)
\(\Leftrightarrow-\left(m-1\right)x^2+2\left(m+2\right)x+3m\ge0\), mọi x thuộc (-\(-\infty;2\) ]
\(\Leftrightarrow m\left(-x^2+2x+3\right)\ge-x^2-4x\), mọi x thuộc (-\(-\infty;2\) ]\(\Leftrightarrow m\le g\left(x\right)\), mọi x thuộc (-\(-\infty;2\) ] (Trong đó \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\))
\(\Leftrightarrow m\le Min_{\left(-\infty;-2\right)}g\left(x\right)\)
Xét hàm số \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\) trên đoạn (-\(-\infty;2\) ]
\(\Rightarrow g'\left(x\right)=\frac{-6\left(x^2+x+2\right)}{\left(-x^2+2x+3\right)^2}=\frac{-6\left(x+\frac{1}{2}\right)^2+\frac{7}{4}}{\left(-x^2+2x+3\right)^2}<0\),mọi x thuộc (-\(-\infty;2\) ]
\(\Rightarrow g\left(x\right)\) là hàm số nghịch biến trên (-\(-\infty;2\) ]
\(\Rightarrow Min_{\left(-\infty;-2\right)}g\left(x\right)=g\left(-2\right)=-\frac{4}{5}\)
Vậy \(m\le-\frac{4}{5}\) thì hàm số đồng biến trên khoảng \(\left(-\infty;-2\right)\)

*Xét hàm số: y= -x3 + 2x2 – x – 7
Tập xác định: D = R
\(y'\left(x\right)=-3x^2+4x-1\); \(y'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
y’ > 0 với và y’ < 0 với \(x \in ( - \infty ,{1 \over 3}) \cup (1, + \infty )
Vậy hàm số đồng biến trong (\(\dfrac{1}{3}\),1)(\(\dfrac{1}{3}\),1) và nghịch biến trong (−∞,13)∪(1,+∞)(−∞,13)b) Xét hàm số: \(y=\dfrac{x-5}{1-x}\).
Tập xác định: D = R{1}
\(y'=\dfrac{-4}{\left(1-x\right)^2}< 0,\forall x\in D\)
Vậy hàm số nghịch biến trong từng khoảng (-∞,1) và (1, +∞)

Chọn B
Hàm số xác định ∀x ≠ -5
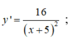
y' xác định ∀x ≠ -5 . Bảng xét dấu y’:
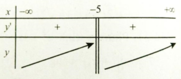
Vậy hàm số đồng biến trên các khoảng (-∞; -5) và (-5; +∞)

\(y'=-x^2+2\left(a-1\right)x+a+3\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x\in\left(0;3\right)\) ta có:
\(-x^2+2\left(a-1\right)x+a+3\ge0\)
\(\Leftrightarrow\left(2x+1\right)a\ge x^2+2x-3\)
\(\Rightarrow a\ge\dfrac{x^2+2x-3}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) với \(x\in\left(0;3\right)\)
\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\Rightarrow a\ge\dfrac{12}{7}\)


y'=3/5*5x^4-3*4x^3+4*3x^2
=3x^4-12x^3+12x^2
=3x^2(x^2-4x+4)=3x^2(x-2)^2>=0
=>Hàm số đồng biến trên R