Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=\dfrac{-3-m}{\left(x-1\right)^2}\) ; \(y\left(2\right)=m+5\) ; \(y'\left(2\right)=-m-3\)
Phương trình tiếp tuyến tại điểm có hoành độ \(x=2\):
\(y=\left(-m-3\right)\left(x-2\right)+m+5\)
\(\Leftrightarrow y=-\left(m+3\right)x+3m+11\)
Để tiếp tuyến cắt 2 trục tạo thành tam giác \(\Rightarrow m\ne\left\{-3;-\dfrac{11}{3}\right\}\)
Gọi A và B lần lượt là giao điểm của tiếp tuyến với Ox và Oy
\(\Rightarrow A\left(\dfrac{3m+11}{m+3};0\right)\) ; \(B\left(0;3m+11\right)\)
\(\Rightarrow OA=\left|\dfrac{3m+11}{m+3}\right|\) ; \(OB=\left|3m+11\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{25}{2}\Rightarrow\dfrac{\left(3m+11\right)^2}{\left|m+3\right|}=25\)
\(\Leftrightarrow\left(3m+11\right)^2=25\left|m+3\right|\Rightarrow\left[{}\begin{matrix}\left(3m+11\right)^2=-25\left(m+3\right)\\\left(3m+11\right)^2=25\left(m+3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9m^2+91m+196=0\\9m^2+41m+46=0\end{matrix}\right.\) \(\Rightarrow m=...\)

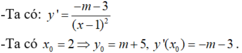
- Phương trình tiếp tuyến Δ của C m tại điểm có hoành độ x 0 = 2 là:
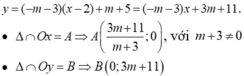
- Suy ra diện tích tam giác OAB là:
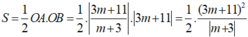
- Theo giả thiết bài toán ta suy ra:
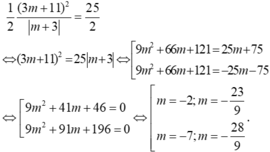
Chọn A.

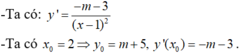
- Phương trình tiếp tuyến Δ của C m tại điểm có hoành độ x 0 = 2 là:
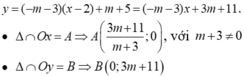
- Suy ra diện tích tam giác OAB là:
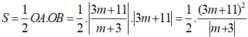
- Theo giả thiết bài toán ta suy ra:
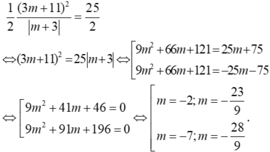
Chọn A.

Phương trình hoành độ giao điểm:
\(x^2-mx+m-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-m+1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=m-1\end{matrix}\right.\) \(\Rightarrow m\ne2\)
\(y'=2x-m\Rightarrow\left\{{}\begin{matrix}y'\left(1\right)=2-m\\y'\left(m-1\right)=m-2\end{matrix}\right.\)
\(y'\left(1\right).y'\left(m-1\right)=-1\)
\(\Leftrightarrow\left(2-m\right)\left(m-2\right)=-1\Leftrightarrow\left(m-2\right)^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=1\\m-2=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=3\end{matrix}\right.\)

a) Gọi M' (x₁' ; y₁' ), N' (x₂' ; y₂ )
* M' là ảnh của M qua phép F, nên toạ độ M' thoả:
{x₁' = x₁.cosα – y₁.sinα + a
{y₁' = x₁.sinα + y₁.cosα + b
* N' là ảnh của N qua phép F, nên toạ độ N' thoả:
{x₂' = x₂.cosα – y₂.sinα + a
{y₂' = x₂.sinα + y₂.cosα + b
b) * Khoảng cách d giữa M và N là:
d = MN = √ [(x₂ - x₁)² + (y₂ - y₁)²]
* Khoảng cách d' giữa M' và N' là:
d' = M'N' = √ [(x₂' - x₁' )² + (y₂' - y₁' )²]
= √ {[x₂.cosα – y₂.sinα + a - (x₁.cosα – y₁.sinα + a)]² + [x₂.sinα + y₂.cosα + b - (x₁.sinα + y₁.cosα + b)]²}
= √ {[cosα(x₂ - x₁) - sinα(y₂ - y₁)]² + [sinα(x₂ - x₁) + cosα(y₂ - y₁)]²}
= √ [(x₂ - x₁)².(cos²α + sin²α) + (y₂ - y₁)².(cos²α + sin²α)]
= √ [(x₂ - x₁)² + (y₂ - y₁)²]
c) Phép F là phép dời hình vì: MN = M'N' = √ [(x₂ - x₁)² + (y₂ - y₁)²]
d) Khi α = 0 ⇒ cosα = 1, sinα = 0
Suy ra:
{x' = x + a
{y' = y + b
Đây là biểu thức toạ độ của phép tịnh tiến. Vậy F là phép tịnh tiến

Ta có: 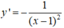
- Lấy điểm M(x0;y0) ∈ (C).
- Phương trình tiếp tuyến tại điểm M là:
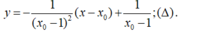
+ Giao với trục hoành: 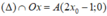
+ Giao với trục tung: 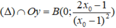
- Ta có:
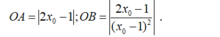
- Theo giả thiết tam giác OAB có diện tích bằng 2 nên: