

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
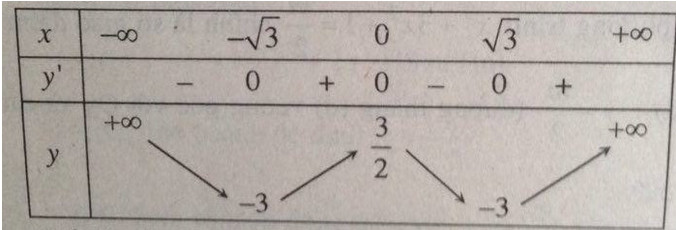
Đồ thị hàm số:
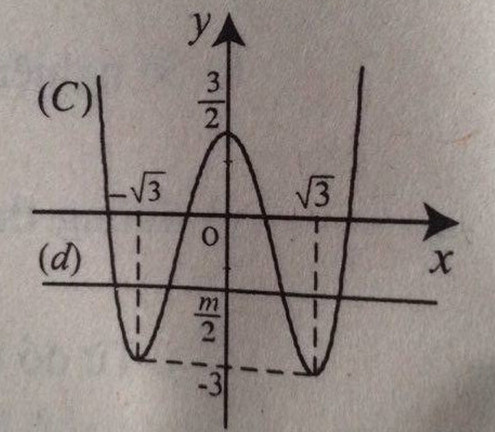
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm

a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
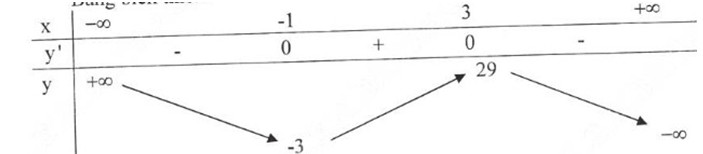
Đồ thị hàm số:
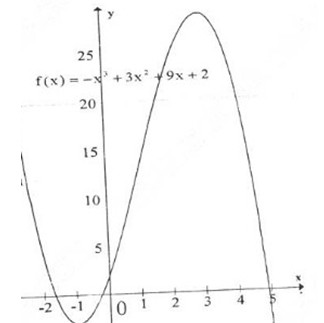
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

Biến đổi :
\(\frac{8\cos x}{3\sin^2x+2\sqrt{3}\sin x\cos x+\cos x^2}=\frac{8\cos x}{\left(\sqrt{3}\sin x+\cos x\right)^2}\)
Giả sử :
\(8\cos x=a\left(\sqrt{3}\sin x+\cos x\right)+b\left(\sqrt{3}\cos x-\sin x\right)=\left(a\sqrt{3}-b\right)\sin x+\left(a+b\sqrt{3}\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có hệ :
\(\begin{cases}a\sqrt{3}-b=0\\a+b\sqrt{3}=8\end{cases}\)\(\Leftrightarrow\begin{cases}a=2\\b=2\sqrt{3}\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2}{\sqrt{3}\sin x-\cos x}-\frac{2\sqrt{3}\left(\left(\sqrt{3}\cos x-\sin x\right)\right)}{\sqrt{3}\sin x-\cos x}\)
Trong đó :
\(F\left(x\right)=\int\frac{2dx}{\sqrt{3}\sin x+\cos x}-\frac{2\sqrt{3}\left(\sqrt{3}\cos x-\sin x\right)dx}{\sqrt{3}\sin x+\cos x}=\frac{1}{2}\ln\left|\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)\right|-\frac{2\sqrt{3}}{\sqrt{3}\sin x+\cos x}+C\)

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2

Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
- Bảng biến thiên:
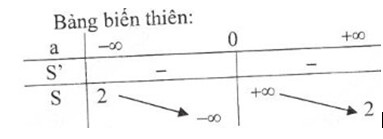
Đồ thị hàm số:
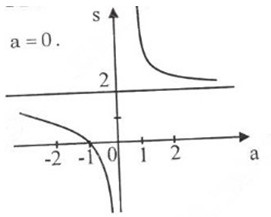
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
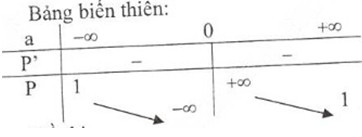
Đồ thị hàm số:
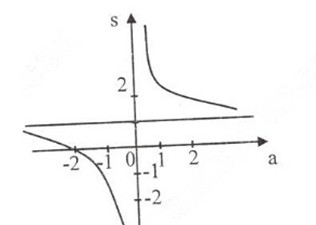
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.