Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta ABC=\Delta DEF\)nên DE = AB ; EF = BC (2 cạnh tương ứng)
Theo gt và cmt,ta có : 2AB = AC + 9 => 2AB - AC = 9
=>\(\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{7}=\frac{2AB}{8}=\frac{2AB-AC}{8-5}=\frac{9}{3}=3\Rightarrow BC=3.3=9\)

Theo đề ta có:
AB+DF-EF=12
AB=DE
BC=EF
AC=DF
Ta thay AC là DF thì ta có AB tỉ lệ thuận với 5,DF tỉ lệ thuận với 7,EF tỉ lệ thuận với 9
\(\Rightarrow\frac{AB}{5}=\frac{DF}{7}=\frac{EF}{9}\)và AB + DF - EF = 12
Theo tính chất dãy tỉ số bằng nhau ta có
\(\frac{AB}{5}=\frac{DF}{7}=\frac{ÈF}{9}=\frac{AB+DF-EF}{5+7-9}=\frac{12}{3}=4\)
\(\Rightarrow\hept{\begin{cases}AB=4\cdot5=20\\DF=4\cdot7=28\\ÈF=4\cdot9=36\end{cases}}\)
Vì DF=28 nên AC =28
Vì EF=36 nên BC=36
Chu vi tam giác ABC là
20+28+36=84
Đúng thì cho mình nha
Gọi a,b,c lần lượt là độ dài AB,AC,BC.
Vì tam giác ABC=tam giác DEF,nên BC=EF(2 cạnh tương ứng)
Ta có:
a/5=b/7=c/9 và a+b-c=12
áp dụng t/c dãy tỉ số bằng nhau:
a/5=b/7=c/9=a+b-c/5+7-9=12/3=4
.a/5=4,nên a=5*4=20.
.b/7=4,nên b=7*4=28.
. c/9=4,nên c=9*4=36.
.AB=20cm,AC=28cm,BC=36cm.
Vậy:chu vi tam giác ABC là:20+28+36=84(cm).

Gọi các cạnh của tam giác lần lượt là `x,y,z (x,y,z \ne 0)`
Các cạnh của tam giác lần lượt tỉ lệ với `2:4:5`
Nghĩa là: `x/2=y/4=z/5`
Chu vi các cạnh của tam giác là `44 cm`
`-> x+y+z=44`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/4=z/5=(x+y+z)/(2+4+5)=44/11=4`
`=>`\(\left\{{}\begin{matrix}\dfrac{x}{2}=4\\\dfrac{y}{4}=4\\\dfrac{z}{5}=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=4\cdot2=8\\y=4\cdot4=16\\z=4\cdot5=20\end{matrix}\right.\)
Vậy, các cạnh của tam giác lần lượt là `8 cm, 16 cm, 20 cm.`

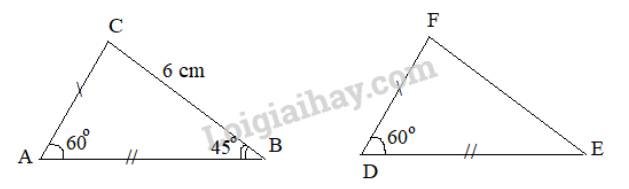
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

1) Ta có hình vẽ sau:
D E K F 1 1 2 2
Vì DE // FK nên \(\widehat{D_1}\) = \(\widehat{F_1}\) (so le trong) ; \(\widehat{D_2}\) = \(\widehat{F_2}\) (so le trong)
Xét ΔDEF và ΔDKF có:
\(\widehat{D_1}\) = \(\widehat{F_1}\) (cm trên)
DF : Cạnh chung
\(\widehat{D_2}\) = \(\widehat{F_2}\) (cm trên)
\(\Rightarrow\) ΔDEF = ΔDKF(g.c.g)
\(\Rightarrow\) \(\widehat{DEF}\) = \(\widehat{DKF}\) (2 góc tương ứng) (đpcm)
2) Ta có hình vẽ sau:
A B C 1 2 F E
Xét ΔABC và ΔAEF có:
AE = AB (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)
AF = AC (gt)
\(\Rightarrow\) ΔABC = ΔAEF (c.g.c)
\(\Rightarrow\) \(\widehat{ACB}\) = \(\widehat{EFA}\) (2 góc tương ứng)
Mà 2 góc này lại ở vị trí so le trong nên
\(\Rightarrow\) BC // EF (đpcm)
Giải:
Ta có: \(\frac{AB}{4}=\frac{AC}{5}=\frac{EF}{7}\)
Vì \(\Delta ABC=\Delta DEF\Rightarrow BC=EF;AB=DE\) ( cạnh t/ứng )
\(\Rightarrow\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{7}\) và \(2AB-AC=9\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{7}=\frac{2AB}{8}=\frac{2AB-AC}{8-5}=\frac{9}{3}=3\)
+) \(\frac{BC}{7}=3\Rightarrow BC=21\)
Vậy BC = 21
ân nhân cứu mạng