Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

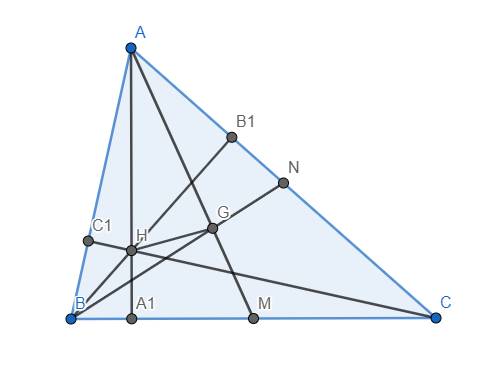
A B C A1 B1 C1 H x y z
Đặt AA1 = a , BB1 = b , CC1 = c , HA1 = x , HB1 = y , HC1 = z (với a,b,c,x,y,z > 0)
a) Đầu tiên , ta cần chứng minh : \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) .
Thật vậy : \(\frac{x}{a}=\frac{x.BC}{a.BC}=\frac{S_{HBC}}{S_{ABC}}\); \(\frac{y}{b}=\frac{y.AC}{b.AC}=\frac{S_{AHC}}{S_{ABC}}\); \(\frac{z}{c}=\frac{z.AB}{c.AB}=\frac{S_{ABH}}{S_{ABC}}\)
\(\Rightarrow\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Ta có : \(\frac{AA_1}{HA_1}+\frac{BB_1}{HB_1}+\frac{CC_1}{HC_1}=\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right).1=\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right).\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)\)
\(\ge\left(1+1+1\right)^2=9\)(áp dụng bđt Bunhiacopxki)
Vậy ta có đpcm
b) Ta có : \(\frac{HA_1}{HA}+\frac{HB_1}{HB}+\frac{HC_1}{HC}=\frac{x}{a-x}+\frac{y}{b-y}+\frac{z}{c-z}=\frac{1}{\frac{a}{x}-1}+\frac{1}{\frac{b}{y}-1}+\frac{1}{\frac{c}{z}-1}\)
Áp dụng bđt \(\frac{m^2}{i}+\frac{n^2}{j}+\frac{p^2}{k}\ge\frac{\left(m+n+p\right)^2}{i+j+k}\)(bạn tự chứng minh)
Ta có : \(\frac{1^2}{\frac{a}{x}-1}+\frac{1^2}{\frac{b}{y}-1}+\frac{1^2}{\frac{c}{z}-1}\ge\frac{\left(1+1+1\right)^2}{\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right)-3}\ge\frac{9}{9-3}=\frac{3}{2}\)
(Từ câu a. ta có \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\ge9\))
Vậy ta có đpcm

O A B C B1 A1 H K C1 M E N 1
a, Có : ^BCK = ^BAK ( chắn cung BK )
^BAK = ^BCH (Phụ ^ABC)
=> ^HCA1 = ^A1CK
=> CA1 là phân giác ^HCK
Tam giác HCK có CA1 vừa là đường cao vừa là phân giác
=> \(\Delta\)HCK cân tại C
=> CA1 là trung tuyến
=> A1 là trung điểm HK
b,\(\frac{HA}{AA_1}+\frac{HB}{BB_1}+\frac{HC}{CC_1}=1-\frac{HA_1}{AA_1}+1-\frac{HB_1}{BB_1}+1-\frac{HC_1}{CC_1}\)
\(=3-\frac{S_{BHC}}{S_{ABC}}-\frac{S_{AHC}}{S_{ABC}}-\frac{S_{AHB}}{S_{ABC}}\)
\(=3-1\)
\(=2\)
c,D \(OM\perp BC\)tại M nên M là trung điểm BC
Xét \(\Delta\)BB1C vuông tại B1 có B1M là trung tuyến
=> B1M = MB = MC
=> ^MBB1 = ^MB1B
và ^MB1C = ^MCB1
Mà ^B1AE = ^B1BC (Chắn cung EC)
^MB1C = ^AB1N (đối đỉnh)
^BB1M + ^CB1M = 90o
=> ^NAB1 + ^NB1A = 90o
=> \(B_1N\perp AE\)
Theo hệ thức lượng trong tam giác vuông có:
\(AB_1^2=AN.AE\)
\(EB_1^2=EN.EA\)
\(\Rightarrow\frac{AB_1^2}{EB_1^2}=\frac{AN.AE}{EN.EA}=\frac{AN}{EN}\)

1) Áp dụng BĐT Cô-si dạng \(\sqrt{ab}\le\frac{a+b}{2}\) cho 2 số dương \(y-1\)và 1
\(x\sqrt{y-1}=x\sqrt{1.\left(y-1\right)}\le x.\frac{1+y-1}{2}=\frac{xy}{2}\)(1)
Tương tự ta có \(y\sqrt{x-1}\le\frac{xy}{2}\)(2)
Cộng (1) và (2) vế theo vế ta suy ra đpcm.
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x-1=1\\y-1=1\end{cases}\Leftrightarrow x=y=2}\)

Vẽ các đường kính AM, BN, CP của (O). Dễ cm được BMCH, CNAH,APBH là các hình bình hành => AH = CN; BH = CM; CH = BM
=> AH + BH + CH = CN + CM + BM
Vì BC cố định nên CN không đổi => (AH + BH + CH) max khi (CM + BM) max. Ta sẽ cm rằng điều đó xảy ra khi M trùng điểm chính giữa cung nhỏ BC.
Thật vậy gọi Q là điểm chính giữa cung nhỏ BC. Kéo dài BQ đoạn QD = BQ = CQ, kéo dài BM đoạn ME = MC => BD = BQ + CQ = 2BQ và BE = BM + CM
Vì tg CQD cân tại Q => ^BDC = ^QCD = ^BQC/2
Tương tự tg CME cân tại M => ^BEC = ^MCE = ^BMC/2
Mà ^BMC = ^BQC => ^BEC = ^BDC => B,C,D,E cùng thuộc đường tròn đường kính BD => BE =< BD <=> BM + CM =< 2BQ => (BM + CM)
Max = 2BQ xảy ra khi E trùng D hay khi M trùng Q khi đó A là điểm chính giữa cung lớn BC