Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 . Chia :( x3 + 5x2 - 4x - 20) cho ( x2 + 3x - 10) ta được x+ 2
Chia :( x3 + 5x2 - 4x - 20) cho ( x2 + 7x + 10) ta được x - 2
Do đó , ta có :
\(\dfrac{1}{x^2+3x-10}=\dfrac{x+2}{\left(x^2+3x-10\right)\left(x+2\right)}=\dfrac{x+2}{x^3+5x^2-4x-20}\)
Và : \(\dfrac{x}{x^2+7x+10}=\dfrac{x\left(x-2\right)}{\left(x^2+7x+10\right)\left(x-2\right)}=\dfrac{x^2-2x}{x^3+5x^2-4x-20}\)
Bài 2 . a) Ta có :
\(\dfrac{x-1}{x^3+1}\)( giữ nguyên)
\(\dfrac{2x}{x^2-x+1}=\dfrac{2x\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{2x^2+2x}{x^3+1}\)
\(\dfrac{2}{x+1}=\dfrac{2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{2x^2-2x+2}{x^3+1}\)
b) Ta có MTC = x2( y - z)2
Ta có :
\(\dfrac{x+y}{x\left(y-z\right)^2}=\dfrac{x^2+xy}{x^2\left(y-z\right)^2}\)
\(\dfrac{y}{x^2\left(y-z\right)^2}\)( giữ nguyên )
\(\dfrac{z}{x^2}=\dfrac{z\left(y-z\right)^2}{x^2\left(y-z\right)^2}\)

a) Tìm MTC: x3 – 1 = (x – 1)(x2 + x + 1)
Nên MTC = (x – 1)(x2 + x + 1)
Nhân tử phụ:
(x3 – 1) : (x3 – 1) = 1
(x – 1)(x2 + x + 1) : (x2 + x + 1) = x – 1
(x – 1)(x2+ x + 1) : 1 = (x – 1)(x2 + x + 1)
Qui đồng:
b) Tìm MTC: x + 2
2x – 4 = 2(x – 2)
6 – 3x = 3(2 – x)
MTC = 6(x – 2)(x + 2)
Nhân tử phụ:
6(x – 2)(x + 2) : (x + 2) = 6(x – 2)
6(x – 2)(x + 2) : 2(x – 2) = 3(x + 2)
6(x – 2)(x + 2) : -3(x – 2) = -2(x + 2)
Qui đồng:

Lời giải:
Ta có: \(\frac{2}{2x^2+7x-15}=\frac{2}{x(2x-3)+5(2x-3)}=\frac{2}{(2x-3)(x+5)}\)
\(\frac{x}{x^2+3x-10}=\frac{x}{x^2+5x-2x-10}=\frac{x}{x(x+5)-2(x+5)}=\frac{x}{(x-2)(x+5)}\)
Do đó khi quy đồng thì mẫu thức chung của 2 phân số này là:
\((x+5)(2x-3)(x-2)=2x^3+3x^2-29x+30\)
Ta có đpcm.


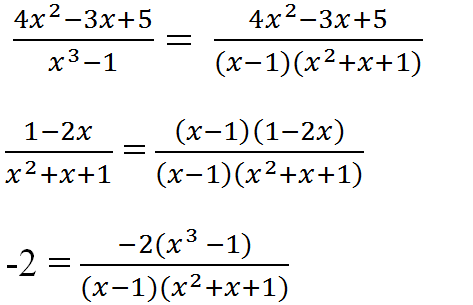
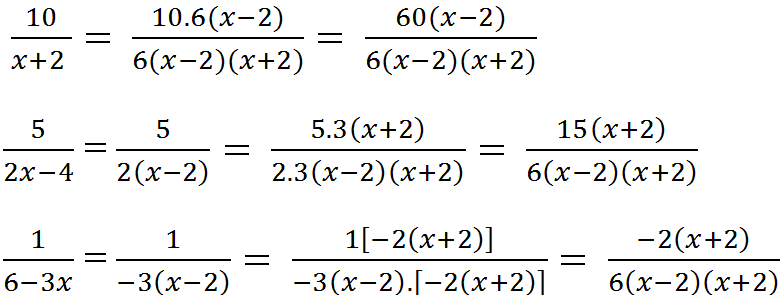
Tại sao lại là x+2 và x-2