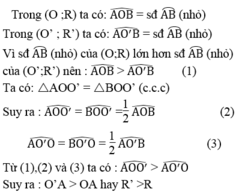Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, OA = OI = O'A = AI
O'AO = 90
=> AOIO' là hình vuông
b, cung AI = 90 độ ( cả 2 cái )
c, Chúng = nhau
xin đại ca kí chữ kí cho em ở chỗ li-ke cho em nha
xin chân thành cảm ơn đại ca

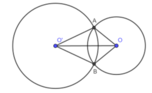
a: Xét tứ giác OAO'B có
OA=O'A=O'B=OB=R
nên OAO'B là hình thoi
b: Xét ΔOAO' có OA=O'A=OO'=R
nên ΔOAO' đều
=>\(\widehat{OAO'}=60^0\)
AOBO' là hình thoi
=>\(\widehat{OBO'}=\widehat{OAO'}=60^0\) và \(\widehat{AOB}=\widehat{AO'B}\)
AOBO' là hình thoi
=>\(\widehat{AOB}+\widehat{OAO'}=180^0\)
=>\(\widehat{AOB}=120^0\)
=>\(\widehat{AO'B}=120^0\)
Xét (O) có
\(\widehat{AOB}\) là góc ở tâm chắn cung AB
\(\widehat{AOB}=120^0\)
Do đó: sđ cung nhỏ AB=120 độ
sđ cung lớn AB trong (O) là:
360-120=240 độ
Xét (O') có
\(\widehat{AO'B}=120^0\)
\(\widehat{AO'B}\) là góc ở tâm chắn cung AB
Do đó: sđ cung nhỏ AB=120 độ
sđ cung lớn AB trong (O') là:
360-120=240 độ
c: ΔAOO' đều nên \(S_{AOO'}=\dfrac{AO^2\cdot\sqrt{3}}{4}=R^2\cdot\dfrac{\sqrt{3}}{4}\)
AOBO' là hình thoi
=>\(S_{AOBO'}=2\cdot S_{AOO'}\)
=>\(S_{AOBO'}=2\cdot\dfrac{R^2\sqrt{3}}{4}=\dfrac{R^2\sqrt{3}}{2}\)


`a,` Ta có: `AO=OB(=R)`
Và: `AB=R` (giả thiết).
`=>AO=AB=BO`
Xét \(\Delta ABO\) có:
`AO=OB=AB(cmt)`
`=>` \(\Delta ABO\) là tam giác đều.
`b,` Ta có: \(\Delta ABO\) là tam giác đều nên:
`=>` \(\widehat{AOB}=60^0\)
Lại có: \(\widehat{AOB}=\dfrac{1}{2}sđ\stackrel\frown{AnB}\) (góc nội tiếp).
\(\Rightarrow sđ\stackrel\frown{AnB}=2\widehat{AOB}=2\cdot60^0=120^0\)
\(\Rightarrow sđ\stackrel\frown{AmB}=360^0-sđ\stackrel\frown{AnB}=360^0-120^0=240^0\)
`c,` Ta có: \(\widehat{AOB}+\widehat{BOC}=180^0\) (kề bù).
\(\Rightarrow\widehat{BOC}=180^0-\widehat{AOB}=180^0-60^0=120^0\)
Mặt khác: \(sđ\stackrel\frown{BnC}=\widehat{BOC}=120^0\) (góc ở tâm).
\(\Rightarrow sđ\stackrel\frown{CAB}=360^0-sđ\stackrel\frown{BnC}=360^0-120^0=240^0\)

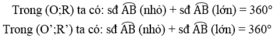
Vì số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’;R’) nên số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O’;R’)
Như vậy, trường hợp này tương tự như giả thiết trong câu a.Chứng minh tương tự ta được R’ > R

ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Hướng dẫn giải:
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3