Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này hơi khó , bạn tự vẽ hình với làm câu a) nhé 😅😅
b)
00' cắt AB tại H
\(\Rightarrow AH=\frac{AB}{2}=\frac{24}{2}=12\)
Áp đụng Pythagore cho tam giác vuông AOH
\(OH=\sqrt{\left(20^2-12^2\right)}=16\)
Pythagore ▲vuông O'AH Áp dụng Pythagore cho tam giác vuông O'AH
\(O'H=\sqrt{\left(15^2-12^2\right)}=9\)
\(\Rightarrow OO'=OH+O'H=16+9=25cm\)
Vậy : OO' dài 25cm

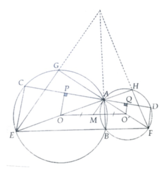
Vẽ OP ⊥ CA; O’Q ⊥ AD suy ra tứ giác OPQO’ là hình thang vuông tại P, Q
a, Kẻ OP; O’Q ⊥ CD do CD ⊥ MA và M là trung điểm của OO’ => AP=AQ => AC=AD
b,i, Chú ý ∆EAF có AB, EG,FI là ba đường cao
ii, Sử dụng CD= 2PQ để lập luận, ta có
Kết luận: CD lớn nhất khi CD//OO’