Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

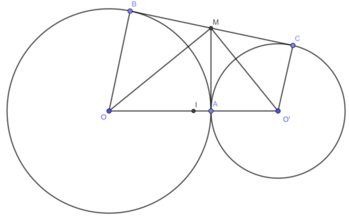
b)ME.MO = MA2 (hệ thức lượng trong MAO vuông)
MF.MO’ = MA2 (hệ thức lượng trong MAO’ vuông)
Suy ra ME.MO = MF.MO’
c)Đường tròn có đường kính BC có tâm M, bán kính MA.OO’ vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).
d)Hình b
Gọi I là trung điểm của OO’, I là tâm của đường tròn có đường kính OO’, IM là bán kính (vì MI là trung tuyến ứng với cạnh huyền của MOO’. IM là đường trung bình của hình thang OBCO’ nên IM // OB // O’C. Do đó IM ⊥ BC.
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I).

Mừng quá. Xong hết rồi. Hơn nửa tiếng bây giờ cũng được đền đáp =))
a) MB = MC (=MA) (giao điểm 2 tiếp tuyến cách đều tiếp điểm)
b) MA = MB = MC => T/g ABC vuông tại A => ^A = 90
T/g OAB cân tại O, có OM là đ/phân giác nên OM cũng là đ cao hay ^ANM = 90
Tương tự, ^APM = 90
=> đpcm
c) MO'/MO = O'C/BM (CMO' ~ BOM) = O'C/CM = CP/MP (CMO' ~ PMC) = MN/MP (PMC = NBM góc vuông - cạnh huyền - góc nhọn so le trong)
=> đpcm
d) Trong t/g vuông OMO' có MA là đường cao, OM^2 = OA.OO' <=> OM = 20 => BM = 12 (Pytago) => BC = 24
e) Dùng ta lét tìm ra OE, EC, còn OC tìm theo pytago trong t/g vuông OBC
f) ABKC là hình chữ nhật => AK cắt BC tại trung điểm M => đpcm

Hướng dẫn giải:
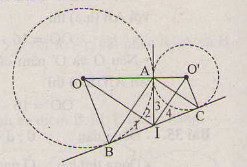
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có IA=IB=IC=12BCIA=IB=IC=12BC.
Do đó tam giác ABC vuông tại A
⇒ˆBAC=90∘⇒BAC^=90∘.
b) Ta có ˆI1=ˆI2;ˆI3=ˆI4I^1=I^2;I^3=I^4 (tính chất hai tiếp tuyến cắt nhau).
Do đó ˆOIO′=90∘OIO′^=90∘ (hai tia phân giác của hai góc kề bù).
c) Ta có AI⊥OO′AI⊥OO′.
Xét tam giác OIO' vuông tại I, ta có:
IA2=OA⋅O′A=9⋅4=36⇒IA=6.IA2=OA⋅O′A=9⋅4=36⇒IA=6.
Do đó BC=12cm.
Nhận xét. Câu a), b) chỉ là gợi ý để làm câu c). Đối với những bài toán có hai đường tròn tiếp xúc, ta thường vẽ thêm tiếp tuyến chung tại tiếp điểm để xuất hiện yếu tố trung gian giúp cho việc tính toán hoặc chứng minh được thuận lợi.

a) Theo tính chất của hai tiếp tuyến cắt nhau ta có IA=IB=IC=12BCIA=IB=IC=12BC.
Do đó tam giác ABC vuông tại A
⇒ˆBAC=90∘⇒BAC^=90∘.
b) Ta có ˆI1=ˆI2;ˆI3=ˆI4I^1=I^2;I^3=I^4 (tính chất hai tiếp tuyến cắt nhau).
Do đó ˆOIO′=90∘OIO′^=90∘ (hai tia phân giác của hai góc kề bù).
c) Ta có AI⊥OO′AI⊥OO′.
Xét tam giác OIO' vuông tại I, ta có:
IA2=OA⋅O′A=9⋅4=36⇒IA=6.IA2=OA⋅O′A=9⋅4=36⇒IA=6.
Do đó BC=12cm.
Nhận xét. Câu a), b) chỉ là gợi ý để làm câu c). Đối với những bài toán có hai đường tròn tiếp xúc, ta thường vẽ thêm tiếp tuyến chung tại tiếp điểm để xuất hiện yếu tố trung gian giúp cho việc tính toán hoặc chứng minh được thuận lợi.

Ta có:
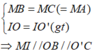
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM

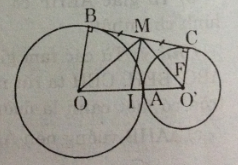
Học online 123 hỏi đáp tun cậy của h/s
ủa bn vừa nãy nói nghĩa là sao vậy