Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

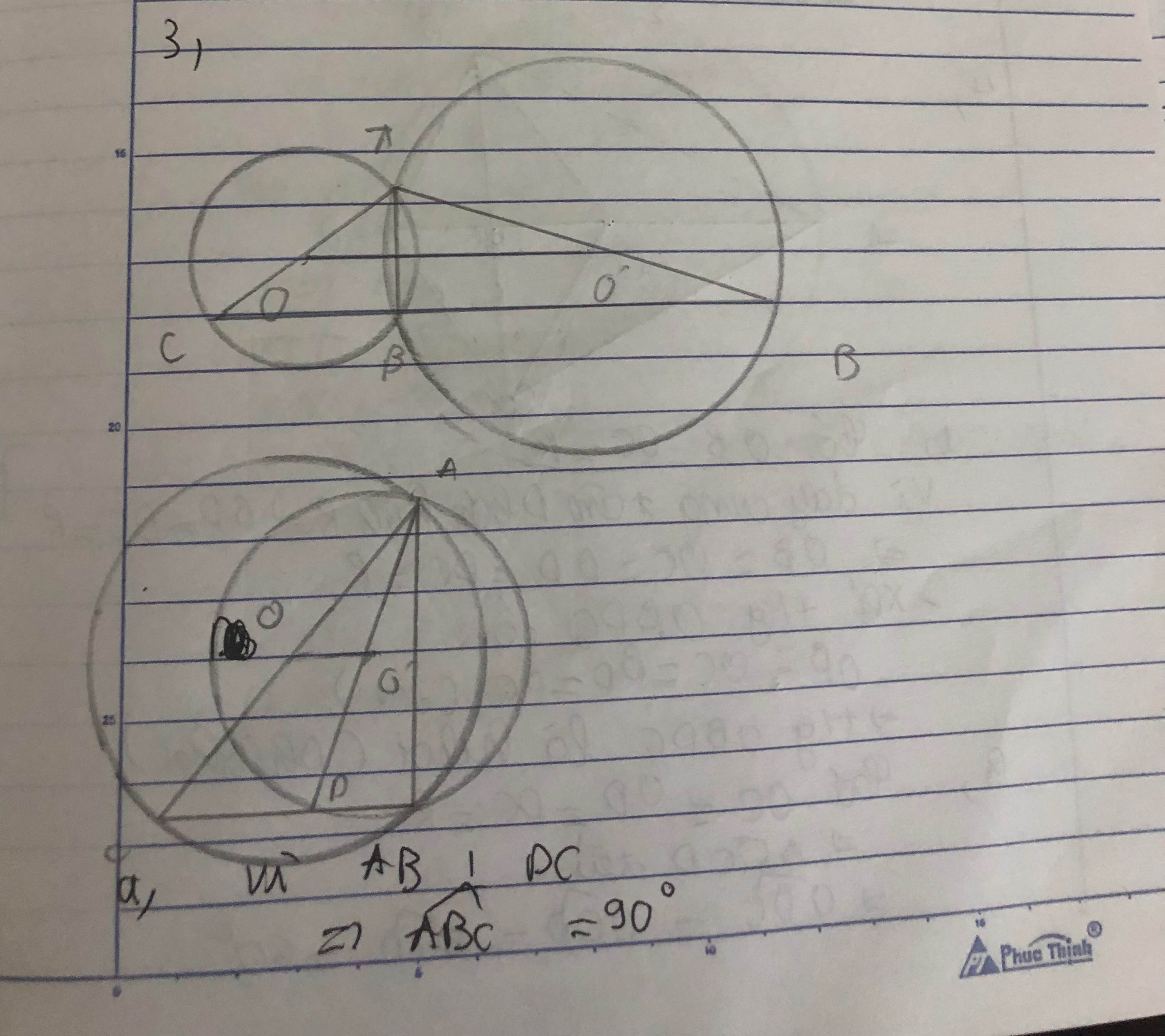
ΔOBC cân tại O nên \(\widehat{BOC}=180^0-2\cdot\widehat{OBC}\)
ΔBO'D cân tại O' nên \(\widehat{BO'D}=180^0-2\cdot\widehat{O'BD}\)
mà \(\widehat{OBC}=\widehat{O'BD}\)
nên \(\widehat{BOC}=\widehat{BO'D}\)

???ng tr�n c: ???ng tr�n qua B_1 v?i t�m O ???ng tr�n d: ???ng tr�n qua D_1 v?i t�m O' ?o?n th?ng h: ?o?n th?ng [A, D] ?o?n th?ng i: ?o?n th?ng [A, C] ?o?n th?ng j: ?o?n th?ng [A, B] ?o?n th?ng k: ?o?n th?ng [D, B] ?o?n th?ng l: ?o?n th?ng [B, C] ?o?n th?ng m: ?o?n th?ng [B, Q] ?o?n th?ng n: ?o?n th?ng [P, B] O = (-2.32, 3.4) O = (-2.32, 3.4) O = (-2.32, 3.4) O' = (2.26, 3.86) O' = (2.26, 3.86) O' = (2.26, 3.86) ?i?m A: Giao ?i?m c?a c, d ?i?m A: Giao ?i?m c?a c, d ?i?m A: Giao ?i?m c?a c, d ?i?m B: Giao ?i?m c?a c, d ?i?m B: Giao ?i?m c?a c, d ?i?m B: Giao ?i?m c?a c, d ?i?m D: Giao ?i?m c?a c, f ?i?m D: Giao ?i?m c?a c, f ?i?m D: Giao ?i?m c?a c, f ?i?m C: Giao ?i?m c?a d, g ?i?m C: Giao ?i?m c?a d, g ?i?m C: Giao ?i?m c?a d, g ?i?m Q: Trung ?i?m c?a A, D ?i?m Q: Trung ?i?m c?a A, D ?i?m Q: Trung ?i?m c?a A, D ?i?m P: Trung ?i?m c?a A, C ?i?m P: Trung ?i?m c?a A, C ?i?m P: Trung ?i?m c?a A, C

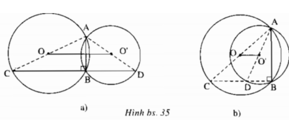
∠ (ABC) = 90 ° nên A, O, C thẳng hàng.
∠ (ABD) = 90 ° nên A, O’, D thẳng hàng.
OO’ là đường trung bình của tam giác ∆ ACD nên OO’ = 1/2CD.

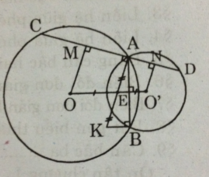 Kẻ OM ⊥ AD.
Kẻ OM ⊥ AD.
Theo tính chất đường kính vuông góc với một dây, ta có: MA = MC
Tương tự, kẻ O'N ⊥ AD => NA = ND.
Ta có:
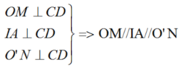
Vậy tứ giác OMNO' là hình thang vuông.
Ta còn có: IO = IO' (gt) và IA // OM
Do đó IA là đường trung bình của hình thang OMNO'.
=> AM = AN hay 2AM = 2AN
Hay AC = CD (đpcm)
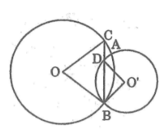


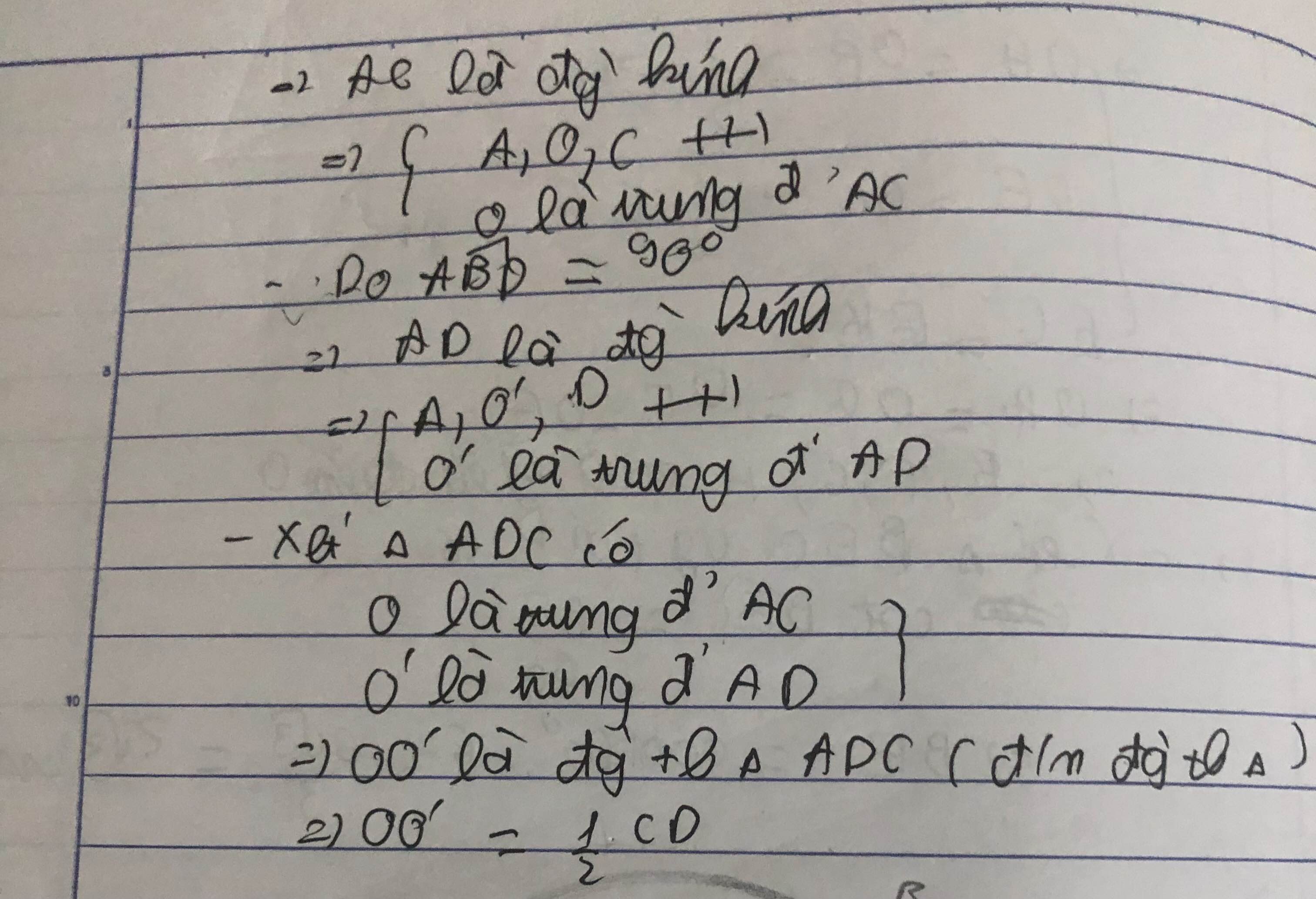
BOC=BO’D
vì C, B cùng thuộc đường tròn (O) => OB=OC => tam giác OBC cân tại O => góc OCB= góc OBC (1)
tương tự góc O'BD= góc O'DB (2)
vì BD là tia pg của góc OBO' => góc OBC= góc DBO' (3)
từ (1) , (2) , (3)=> góc OBC=OCB=O'DB=O'BD
=> góc BOC = góc DO'B