Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

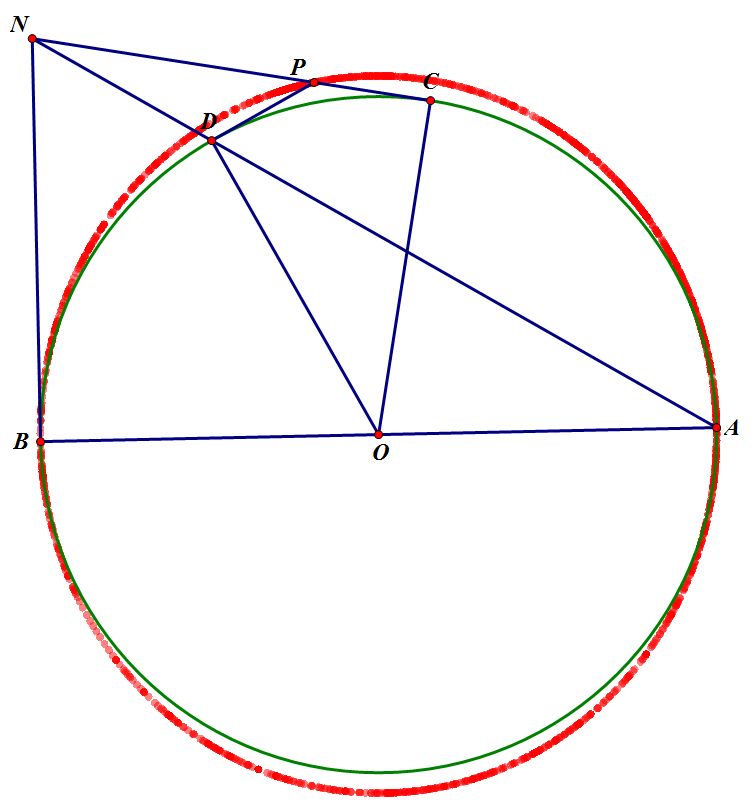
1). Gọi MN giao PQ tại T. Theo định lí Thales, ta có T P T C = T D T B = T C T Q .
Từ đó T C 2 = T P . T Q .
Do TC là tiếp tuyến của (O), nên T C 2 = T M . T N .
Từ đó T M . T N = T C 2 = T P . T Q , suy ra tứ giác MNPQ nội tiếp.

(a) Gọi F là giao điểm của AE và BP.
Từ tính chất góc nội tiếp và đường cao của tam giác vuông ta dễ thấy :∠AEC = ∠ABC = ∠BPCvậy tứ giác CPFE nội tiếp. Từ đó suy ra ∠CPE = ∠CFE, ∠PCE = ∠EFBCộng các đẳng thức góc với chú ý ∠CEP = 90◦ , ta suy ra 90◦ = ∠CPE +∠PCE = ∠CFE +∠EFB = ∠CFB, hay CF ⊥ PB, và do đó CF ∥ AB.Bổ đề. Cho hình thang ABCD, AB ∥ CD. Giả sử AC cắt BD tại O và AD cắt BC tại I. Khi đó, OI đi qua trung điểm AB và CD.CMVẽ đường thẳng EF đi qua O và song song CD.Ta có EO//DC ⇒ OE/DC = AO/AC (1)
OF//DC ⇒ OF/DC = BO/BD (2)
Ta có: AB//DC ⇒ OA/OC = OB/OD
⇒ OA/ (OC + OA) = OB/(OD+ OB) ⇒ OA/AC = OB/BD (3)
Từ (1),(2),(3) ta có OE/DC = OF/DC ⇒ OE = OF
Ta có AB//EF
⇒ AN/EO = IN/IO và BN/FO = IM/KO
⇒ AN/EO = BN/FO ⇒ AN = BN
Tương tự: FE//DC ⇒ EO/DM = IO/IM
và FO/CM = IO/IM ⇒EO/DM=FO/CM ⇒ DM=CM suy ra đường thẳng OI đi qua trung điểm của các cạnh AB và CD.Bổ đề dc CMGọi M' là giao điểm của CB và AE. Áp dụng bổ đề cho hình thang ABFC, ta có M'P đi qua trung điểm AB hay M'P đi qua O. Vậy AE, BC, OP đồng quy tại M', đó là điều phải chứng minh. (b) Áp dụng định lý Menelaus cho tam giác APO với C, M, B thẳng hàng, ta dễ thấy OM/ OP = CA /(CA +2CP) . Từ đó ta có S(M AB)/ S(PAB) = OM/OP = CA/(CA +2CP ). Suy ra S(MAB) = S(PAB) · CA/(CA +2CP)>/= S(PAB) · CA 2can2BC = (BC ·P A )/2 · CA /2 can2BC = 4R^2/ 4can2 = R^2/can2 . Đẳng thức xảy khi PB = can 2R.Hok Tốt =>>>>>>>>>>>>

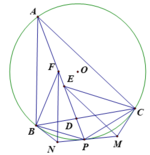
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.

A B C O I M N P Q L K J
Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).

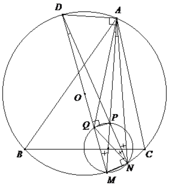
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .