


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Lấy A' đối xứng với A qua d. Khi đó: AM+MB=A'M+MB>=A'B.
Vậy (AM+MB)min <=> A', M, B thẳng hàng.
Cách dựng: Lấy A' đối xứng A qua d, A'B cắt d tại M. M là điểm cần tìm


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).

Đáp án D
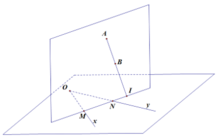
AB và mặt phẳng (Ox, Oy) luôn có điểm chung I
α chứa AB
⇒ I luôn nằm trên giao tuyến của α và (Ox, Oy) (1)
Ta lại có: α thay đổi cắt Ox tại M, Oy tại N
Xét α và (Ox, Oy) có M và N là điểm chung
⇒ MN là giao tuyến của 2 mặt phẳng (2)
(1);(2): M, N, I thẳng hàng
⇒ MN luôn đi qua I cố định

- Kẻ AA’ ( là đường kính của (O) ) suy ra BHCA’ là hình bình hành , cho nên BC đi qua trung điểm I của A’H .
- A’H’ song song với BC ( vì cùng vuông góc với AH )
- Từ đó suy ra BC là đường trung bình của tam giác AHH’ – Có nghĩa là BC đi qua trung điểm của HH’ . Mặt khác AH vuông góc với BC suy ra BC là trục đối xứng của HH’ , hay H và H’ đối xứng nhau qua BC.
Gọi H là giao ba đường cao của tam giác ABC . Kéo dài AH cắt (O;R) tại H’ . Nối CH’
- Chứng minh IH=IH’ . Thật vậy
Ta có : \(\widehat{A}=\widehat{BCH'}\) ( Góc nội tiếp chẵn cung BH’ ).(1)
Mặt khác : \(\begin{cases}CH\perp AB\\CI\perp AH'\end{cases}\)\(\Rightarrow\widehat{A}=\widehat{BCH}\) (2)
Từ (1) và (2) suy ra : \(\widehat{BCH}=\widehat{BCH'}\)
Chứng tỏ tam giác HCH’ là tam giác cân . Do BC vuông góc với HH’ , chứng tỏ BC là đường trung trực của HH’ . Hay H và H’ đối xứng nhau qua BC . Cho nên khi A chạy trên đường tròn (O;R) thì H’ cũng chạy trên (O;R) và H sẽ chạy trên đường tròn (O’;R) là ảnh của đường tròn (O;R) qua phép đối xứng trục BC
- Giới hạn quỹ tích : Khi A trùng với B và C thì tam giác ABC suy biến thành đường thẳng . Vì thế trên đường tròn (O’;R) bỏ đi 2 điểm là ảnh của B,C

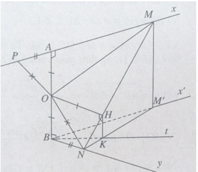
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
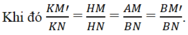
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

Gọi \(\overrightarrow{u},\overrightarrow{v}\) theo thứ tự là vec tơ chỉ phương đơn vị của các tia Ox, Oy, tương ứng cùng hướng với các tia Ox, Oy gọi I là tâm của \(\omega\). Chọn O làm gốc vec tơ điểm và với mỗi điểm X của mặt phẳng, ký hiệu \(\overrightarrow{x}\) để chỉ vec tơ \(\overrightarrow{OX}\). Trung trực OA cắt các đường thẳng \(d_1,d_2\) theo thứ tự tại B, C.
Khi đó B, C cố định và do I nằm trên đường thẳng BC nên \(\overrightarrow{i}=\alpha\overrightarrow{b}+\left(1-\alpha\right)\overrightarrow{c}\)
Mặt khác , theo định lí chiếu ta có :
\(\overrightarrow{m}=2\left(\overrightarrow{i}.\overrightarrow{u}\right).\overrightarrow{u}\) và \(\overrightarrow{n}=2\left(\overrightarrow{i}.\overrightarrow{v}\right).\overrightarrow{v}\)
Gọi P là trung điểm MN. Suy ra \(2\overrightarrow{p}=\overrightarrow{m}.\overrightarrow{n}\). Bởi vậy, với \(b=OB,c=OC\) và \(t=\cos<\left(\overrightarrow{u}\overrightarrow{v}\right)\) thì b, c, t là các hằng số và :
\(\overrightarrow{p}=\left[\alpha.\overrightarrow{b}\overrightarrow{u}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{u}\right].\overrightarrow{u}+\left[\alpha.\overrightarrow{b}\overrightarrow{v}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{v}\right].\overrightarrow{v}\)
\(=\alpha.b\left(\overrightarrow{u}+t\overrightarrow{v}\right)+\left(1-\alpha\right).c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\)
\(=\alpha\overrightarrow{x}+\left(1-\alpha\right)\overrightarrow{y}\)
Trong đó \(\overrightarrow{x}=\overrightarrow{OX}=b\left(\overrightarrow{u}+t\overrightarrow{v}\right)\) và \(\overrightarrow{y}=\overrightarrow{OY}=c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\) là các vec tơ cố định
Suy ra P luôn nằm trên đường thẳng XY cố định khi \(\omega\) thay đổi