Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#)Giải :
A B C D O t t'
a) Vì góc AOC và góc BOD là hai góc đối đỉnh => góc AOC = góc BOD ( = 60o)
Vì góc AOC và góc BOC là hai góc kề bù => góc BOC = 180o - góc AOC = 180o - 60o = 120o
Vì góc BOC và góc AOD là hai góc đối đỉnh => góc BOC = góc AOD ( = 120o)
b) Vì Ot là tia phân giác của góc AOC => góc AOt = góc COt = 60o/2 = 30o
Vì góc AOt và góc BOt' là hai góc đối đỉnh => góc AOt = góc BOt' ( = 30o)
Vì góc COt và góc DOt' là hai góc đối đỉnh => góc COt = góc DOt' ( = 30o)
=> góc BOt' = góc DOt' ( = 30o)
=> Ot' là tia phân giác của góc BOD
C B D A o t t'
Giải
a) +) Vì \(\widehat{AOC}\)và \(\widehat{BOD}\) là 2 góc đối đỉnh
=> \(\widehat{AOC}\) = \(\widehat{BOD}\) = 60o
+) Vì \(\widehat{COB}\) và \(\widehat{BOD}\)là 2 góc kề bù
=> \(\widehat{COB}\)+ \(\widehat{BOD}\)= 180o
Hay \(\widehat{COB}\)+ 60o = 180o
\(\widehat{COB}\) = 180o - 60o = 120o
+) Vì \(\widehat{COB}\)và \(\widehat{AOD}\)là 2 góc đối đỉnh
=> \(\widehat{COB}\)= \(\widehat{AOD}\) = 120o
b) Vì Ot là tia phân giác của \(\widehat{AOC}\)
=> \(\widehat{AOt}\)= \(\widehat{tOC}\)= \(\frac{\text{}\widehat{AOC}}{2}\)= \(\frac{60^o}{2}\)= 30o
Vì \(\widehat{AOt}\)và \(\widehat{BOt'}\)là 2 góc đối đỉnh
=> \(\widehat{AOt}\)= \(\widehat{BOt'}\)= 30o
Vì \(\widehat{COt}\)và \(\widehat{DOt'}\)là 2 góc đối đỉnh
=> \(\widehat{COt}\)= \(\widehat{DOt'}\)= 30o
=> \(\widehat{BOt'}\)= \(\widehat{DOt'}\)( = 30o ) ( 1 )
Trên cùng 1 nửa mặt phẳng bờ chứa tia OD có \(\widehat{DOt'}< \widehat{DOB}\)( vì 30o < 60o )
=> Ot' nằm giữa OB và OD ( 2 )
Từ ( 1 ) và ( 2 ) => Ot' là tia phân giác của \(\widehat{BOD}\)

a) B O D ^ = A O C ^ = 60° (đối đỉnh.).
=> C O B ^ + A O C ^ = 180° (kề bù), => B O C ^ = 180 ° − A O C ^ = 120°
=> A O D ^ = B O C ^ = 120° (đối đỉnh),
b) Vì Ot là phân giác góc AOC nên
A O t ^ = 1 2 A O C ^ = 30°
=> B O t ' ^ = A O t ^ = 30° (đối đỉnh).
Tương tự:
D O t ' ^ = 30 ° ⇒ B O t ' ^ = D O t ' ^
Do đó Ot' là phân giác của B O D ^ .

a) \(\widehat{DOB}=\widehat{AOC}=60^o\) (đối đỉnh)
Ta có : \(\widehat{AOC}+\widehat{BOC}=180^o\) (kề bù)
=> \(\widehat{BOC}=180^o-60^o=120^o\)
\(\widehat{AOD}=\widehat{BOC}=120^o\) (đối đỉnh)
b) Ot là tia p/g của góc AOC nên \(\widehat{tOc}=\frac{1}{2}\widehat{AOC}=30^o\)
Ta có : \(\widehat{tOC}+\widehat{BOC}+\widehat{t'OB}=180^o\) (kề bù)
=> \(30^o+120^o+\widehat{t'OB}=180^o\)
=> \(\widehat{t'OB}=30^o=\frac{1}{2}.60^o=\frac{1}{2}\widehat{BOD}\)
=> Ot' là tia p/g của góc BOD

A B C D O t t'
Bài làm
a) \(\widehat{AOC}\)là:
( 180o + 20o ) : 2 = 100o
\(\widehat{AOD}\)là:
180o - 100o = 80o
Mà \(\widehat{BOD}\)đối đỉnh với \(\widehat{AOC}\)
\(\widehat{BOC}\)đối đỉnh với \(\widehat{AOD}\)
=> \(\widehat{BOD}=100^0\)
=> \(\widehat{BOC}=80^0\)
b) Ta có: \(\widehat{COt}=\widehat{t'OD}\)( hai góc đối đỉnh )
\(\widehat{tOB}=\widehat{t'OA}\)( hai góc đối đỉnh )
Mà \(\widehat{COt}=\widehat{tOB}\)
=> \(\widehat{t'OD}=\widehat{t'OA}\)
=> Ot' là tia phân giác của góc \(\widehat{AOD}\)( đpcm )
# Học tốt #
Bài làm
a) \(\widehat{AOC}\)là:
( 180o + 20o ) : 2 = 100o
\(\widehat{AOD}\)là:
180o - 100o = 80o
Mà \(\widehat{BOD}\)đối đỉnh với \(\widehat{AOC}\)
\(\widehat{BOC}\)đối đỉnh với \(\widehat{AOD}\)
=> \(\widehat{BOD}=100^0\)
=> \(\widehat{BOC}=80^0\)
b) Ta có: \(\widehat{COt}=\widehat{t'OD}\)( hai góc đối đỉnh )
\(\widehat{tOB}=\widehat{t'OA}\)( hai góc đối đỉnh )
Mà \(\widehat{COt}=\widehat{tOB}\)
=> \(\widehat{t'OD}=\widehat{t'OA}\)
=> Ot' là tia phân giác của góc \(\widehat{AOD}\)( đpcm )
# Học tốt #

a) ta có: đường thẳng AB,CD cắt nhau tại O
=> góc AOC = góc BOD = 60 độ ( đối đỉnh)
=> góc BOD = 60 độ
mà góc BOD + góc BOC = 180 độ ( kề bù)
thay số: 60 độ + góc BOC = 180 độ
góc BOC = 180 độ - 60 độ
góc BOC = 120 độ
mà góc BOC = góc AOD = 120 độ ( đối đỉnh)
=> góc AOD = 120 độ
b) ta có: Ot là tia phân giác của góc AOC
ma Ot là tia đối của tia Ot'
=> tt' là tia phân giác của góc AOC
mà góc AOC = góc BOD ( đối đỉnh)
=> tt' là tia phân giác của góc BOD
mà Ot nằm giữa OA;OC và Ot là tia đối của Ot', góc AOC = góc BOD đối đỉnh
=> Ot' nằm giữa OB,OD
mà Ot' thuộc tt'
=> Ot' là tia phân giác của góc BOD
C O B D A t t' 60
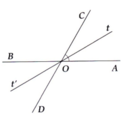

( Hình dễ nên bạn tự vẽ nhé )
)
Mình nghĩ câu b chỉ chứng tỏ là tia phân giác của góc BOD thôi