Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Cách 1:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\( \Leftrightarrow \overrightarrow {KA} = - 2\overrightarrow {KB} \)
Suy ra vecto \(\overrightarrow {KA} \) và vecto\(\;\overrightarrow {KB} \) cùng phương, ngược chiều và \(KA = 2.KB\)
\( \Rightarrow K,A,B\)thẳng hàng, K nằm giữa A và B thỏa mãn: \(KA = 2.KB\)
Cách 2:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\(\begin{array}{l} \Leftrightarrow \left( {\overrightarrow {KB} + \overrightarrow {BA} } \right) + 2\overrightarrow {KB} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} + \overrightarrow {BA} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {KB} = \frac{1}{3}\overrightarrow {AB} \end{array}\)
Vậy K thuộc đoạn AB sao cho \(KB = \frac{1}{3}AB\).
b)
Với O bất kì, ta có:
\(\frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} = \frac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \frac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) = \left( {\frac{1}{3}\overrightarrow {OK} + \frac{2}{3}\overrightarrow {OK} } \right) + \left( {\frac{1}{3}\overrightarrow {KA} + \frac{2}{3}\overrightarrow {KB} } \right) = \overrightarrow {OK} + \frac{1}{3}\left( {\overrightarrow {KA} + 2\overrightarrow {KB} } \right) = \overrightarrow {OK}\)
Vì \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \)
Vậy với mọi điểm O, ta có \(\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} .\)

a)Giả sử điểm K thỏa mãn:
\(\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{CB}\)\(\Leftrightarrow\overrightarrow{KB}+\overrightarrow{BA}+2\overrightarrow{KB}=\overrightarrow{CB}\)
\(\Leftrightarrow3\overrightarrow{KB}=\overrightarrow{CB}-\overrightarrow{BA}\)
\(\Leftrightarrow\overrightarrow{KB}=\overrightarrow{CB}+\overrightarrow{AB}\).
Xác định: \(\overrightarrow{CB}+\overrightarrow{AB}\).
A B C D
Lấy điểm D sao cho B là trung điểm của DC.
\(\overrightarrow{CB}+\overrightarrow{AB}=\overrightarrow{BD}+\overrightarrow{AB}=\overrightarrow{AD}\).
Điểm K xác định sao cho : \(\overrightarrow{KB}=\overrightarrow{AD}\) hay tứ giác AKBD là hình bình hành.
A B C D K
b) Gọi G là trọng tâm tam giác ABC.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+2\overrightarrow{MG}\)\(+2\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\overrightarrow{GC}\).
Giả sử điểm M thỏa mãn:
\(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow4\overrightarrow{MG}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
Điểm M được xác định để \(\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
A B C G T M
Gọi T là trung điểm của AB nên \(\overrightarrow{CG}=2\overrightarrow{GT}\).
Vì vậy điểm M được xác định là trung điểm của GT.

a.
\(\overrightarrow{IA}+2\left(\overrightarrow{IA}+\overrightarrow{AB}\right)=\overrightarrow{0}\Leftrightarrow3\overrightarrow{IA}+2\overrightarrow{AB}=0\)
\(\Leftrightarrow\overrightarrow{AI}=\frac{2}{3}\overrightarrow{AB}\)
Vậy I là điểm nằm trên đoạn thẳng AB sao cho \(AI=\frac{2}{3}AB\)
b.
Gọi G là trọng tâm tam giác ABC
\(\overrightarrow{KG}+\overrightarrow{GA}+2\left(\overrightarrow{KG}+\overrightarrow{GB}\right)=\overrightarrow{CG}+\overrightarrow{GB}\)
\(\Leftrightarrow3\overrightarrow{KG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\Leftrightarrow3\overrightarrow{KG}=\overrightarrow{0}\)
\(\Leftrightarrow\) K trùng G hay K là trọng tâm tam giác
c.
\(\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+2\left(\overrightarrow{MG}+\overrightarrow{GC}\right)=0\)
\(\Leftrightarrow4\overrightarrow{MG}+\overrightarrow{GC}=0\Leftrightarrow\overrightarrow{GM}=\frac{1}{4}\overrightarrow{GC}\)
Vậy M là điểm nằm trên đoạn thẳng CG sao cho \(GM=\frac{1}{4}CG\)

\(K\left(0;y\right)\Rightarrow\overrightarrow{KA}=\left(2;1-y\right)\) ; \(\overrightarrow{KB}=\left(6;-1-y\right)\)
\(\overrightarrow{KA}+\overrightarrow{KB}=\left(8;-2y\right)\)
\(\Rightarrow T=2\sqrt{4+\left(1-y\right)^2}+\sqrt{64+4y^2}\)
\(T=2\left(\sqrt{2^2+\left(1-y\right)^2}+\sqrt{4^2+y^2}\right)\)
\(T\ge2\sqrt{\left(2+4\right)^2+\left(1-y+y\right)^2}=2\sqrt{37}\)
\(T_{min}=2\sqrt{37}\) khi \(\frac{y}{1-y}=\frac{4}{2}\Rightarrow y=\frac{2}{3}\) \(\Rightarrow K\left(0;\frac{2}{3}\right)\)

a) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\)
Vậy bất kì điểm M nào nằm trên mặt phẳng cũng thỏa mãn:
\(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\).
b) Do \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\) nên không tồn tại điểm M thỏa mãn: \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\).
c) \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) nên M là trung điểm của AB.
a,, CÓ \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\Leftrightarrow\overrightarrow{BA}=\overrightarrow{BA}\)
Vậy với mọi điểm M thì đều thõa mãn
b, có \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\Leftrightarrow\overrightarrow{BA}=\overrightarrow{AB}\) ( không thõa mãn)
vậy không có điểm M nào thõa mãn điều kện trên
c, có \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{O}\) \(\Rightarrow\) M là trung điểm của AB
Ta có: 3 + 2
+ 2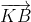 =
= 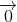 => 3
=> 3 = -2
= -2 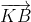 =>
=>  = -
= - 
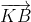
Đẳng thức này chứng tỏ hi vec tơ ,
,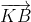 là hai vec tơ ngược hướng, do đó K thuộc đoạn AB
là hai vec tơ ngược hướng, do đó K thuộc đoạn AB
Ta lại có: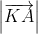 = -
= - 
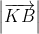 => KA =
=> KA =  KB
KB
Vậy K là điểm chia trong đoạn thẳng AB theo tỉ số