Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Cách 1:
P(x) + Q(x) = \(7{x^3} - 8x + 12 + 6{x^2} - 2{x^3} + 3x - 5\)
\(\begin{array}{l} = (7{x^3} - 2{x^3}) + 6{x^2} + ( - 8x + 3x) + (12 - 5)\\ = 5{x^3} + 6{x^2} - 5x + 7\end{array}\)
Cách 2:
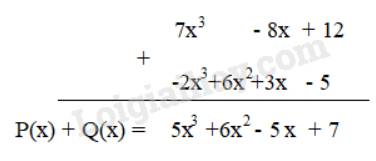

\(P(x) + Q(x) = - 3{x^4} - 8{x^2} + 2x + 5{x^3} - 3{x^2} + 4x - 6\)
\( = - 3{x^4} + 5{x^3} + ( - 8{x^2} - 3{x^2}) + (2x + 4x) - 6\)
\( = - 3{x^4} + 5{x^3} - 11{x^2} + 6x - 6\)
\(P(x) - Q(x) = - 3{x^4} - 8{x^2} + 2x - 5{x^3} + 3{x^2} - 4x + 6\)
\( = - 3{x^4} - 5{x^3} + ( - 8{x^2} + 3{x^2}) + (2x - 4x) + 6\)
\( = - 3{x^4} - 5{x^3} - 5{x^2} - 2x + 6\)

a. P(x) = -3x5 - 7x3 + x2 - 5x + 2
Q(x) = -4x5 - x4 + x3 - x2 - 6x
b. Đa thức P(x) và Q(x) có bậc là 5
d. Q(-1) = -4(-1)5 - (-1)4 + (-1)3 - (-1)2 - 6(-1)
= -4.(-1) + 1 + 1 - 1 + 1 - 6.(-1)
= 12
a) Ta có: \(P\left(x\right)=x^2-5x-3x^5-7x^3+2\)
\(=-3x^5-7x^3+x^2-5x+2\)
Ta có: \(Q\left(x\right)=x^3-6x-x^2-4x^5-x^4\)
\(=-4x^5-x^4+x^3-x^2-6x\)

a)\(P\left(x\right)=x^5+2x^4-9x^3-x\)
\(Q\left(x\right)=5x^4+9x^3+4x^2-14\)
b) Sửa Tìm hệ số cao nhất và hệ số tự do của đa thức Q(x)
hệ số cao nhất :9
hệ số tự do :- 14
c)\(M\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(\Leftrightarrow M\left(x\right)=x^5+2x^4-9x^3-x+5x^4+9x^3+4x^2-14\)
\(M\left(x\right)=x^5+6x^4-x-14\)
d)\(M\left(2\right)=2^5+6.2^4-2-14=32-96-2-14=-80\)
\(M\left(-2\right)=\left(-2\right)^5+6.\left(-2\right)^4+2-14=-32-96+2-14=-140\)
\(M\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^5+6.\left(\dfrac{1}{2}\right)^4-\dfrac{1}{2}-14=\dfrac{1}{32}+\dfrac{3}{8}-\dfrac{1}{2}-14=-\dfrac{475}{32}\)

Ta có: \(f\left(x\right)+g\left(x\right)=x+3x^2\)
\(\Rightarrow h\left(x\right)=x+3x^2=0\)
\(\Leftrightarrow x\left(1+3x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\1+3x=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{-1}{3}\end{cases}}}\)
Vậy.....
Ta có :\(f\left(x\right)=9-x^5+4x-2x^3+x^2-7x^4\)
\(g\left(x\right)=x^5-9+2x^2+7x^4+2x^3-3x\)
\(\Rightarrow h\left(x\right)=f\left(x\right)+g\left(x\right)\)
\(\Rightarrow h\left(x\right)=9-x^5+4x-2x^3+x^2-7x^4+x^5-9+2x^2+7x^4+2x^3-3x\)
\(\Rightarrow h\left(x\right)=3x^2+x\)
Đặt \(3x^2+x=0\Leftrightarrow x\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-\frac{1}{3}\end{cases}}}\)

a)
`P(x)=7x^3+(4x^2-3x^2)-x+5=7x^3+x^2-x+5`
`Q(x)=-7x^3-x^2+2x+(6-8)=-7x^3-x^2+2x-2`
b)
`P(x)+Q(x) = 7x^3+x^2-x+5-7x^3-x^2+2x-2`
`=(7x^3-7x^3)+(x^2-x^2)+(2x-x)+(5-2)`
`=x+3`
`P(x)-Q(x)=7x^3+x^2-x+5-(-7x^3-x^2+2x-2)`
`= 7x^3+x^2-x+5+7x^3+x^2-2x+2`
`=(7x^3+7x^3)+(x^2+x^2)-(x+2x)+(5+2)`
`=14x^3+2x^2-3x+7`
c) `A(x) = P(x)+Q(x)=x+3`
`A(x)=0 <=> x+3=0 <=>x=-3`.

Theo cột dọc:
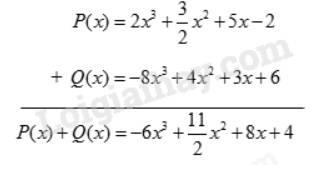
Theo hàng ngang:
\(\begin{array}{l}P(x) + Q(x) = 2{x^3} + \dfrac{3}{2}{x^2} + 5x - 2 + ( - 8){x^3} + 4{x^2} + 3x + 6\\ = (2 - 8){x^3} + (\dfrac{3}{2} + 4){x^2} + (5 + 3)x + ( - 2 + 6)\\ = - 6{x^3} + \dfrac{{11}}{2}{x^2} + 8x + 4\end{array}\)

a: \(P\left(x\right)+Q\left(x\right)=-2x^3-7x^2-2x+4\)
\(P\left(x\right)-Q\left(x\right)=10x^3-7x^2+8x-14\)
b: \(P\left(1\right)=4-7+3-5=-5\)
\(P\left(-1\right)=-4-7-3-5=-19\)
Tham khảo:
Cách 1 :
Ta có P(x) - Q(x)
= 2x3 – 9x2 + 5 – (2x2 + 4x3 – 7x)
= 2x3 – 9x2 + 5 – 2x2 – 4x3 + 7x
= (2x3 – 4x3) + (-9x2 – 2x2) + 7x + 5
= -2x3 – 11x2 + 7x + 5
Cách 2 :
P(x) = 2x3 – 9x2 + 5
Q(x) = 4x3 + 2x2 – 7x