Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn phương án (D) :
Quỹ tích các điểm M nhìn đoạn thẳng AB dưới 1 góc \(120^0\) là hai cung chứa góc \(120^0\) (đối xứng nhau) dựng trên hai điểm A, B.
Chọn (D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).
Lấy đối xứng qua đường thẳng AB, ta được cung chứa góc thứ hai thỏa mãn bài toán.
Chú ý : Cung nhỏ AB trong cách dựng trên là cung chứa góc \(120^0\)
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc = 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
Dựng đoạn thẩng AB bằng 3cm dựng góc xAB =55* dựng tia AY vuông góc vs tia Ax dựng đg trung trực d của đoạn thẳng AB/ d cắt Ay tại O . Dựng đg tròn tâm O bán kính OA cung AmB là góc 55 độ cần dựng
Điểm M nằm trên cung chứa góc 90 độ dựng trên đoạn AB <=> góc AMB=90.
=> tam giác AMB vuông tại M => áp dụng định lí py ta go ta có: \(MA^2+MB^2=AB^2=10^2=100\)(CM)
a: Ta có: ΔOAC vuông tại O
=>\(OA^2+OC^2=AC^2\)
=>\(AC^2=R^2+R^2=2R^2\)
=>\(AC=R\sqrt{2}\)
b: Xét (O) có
\(\widehat{BKM}\) là góc có đỉnh ở trong đường tròn chắn hai cung BM và CA
=>\(\widehat{BKM}=\dfrac{1}{2}\left(sđ\stackrel\frown{BM}+sđ\stackrel\frown{CA}\right)\)
=>\(\widehat{IKM}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BM}+sđ\stackrel\frown{BC}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{MC}\left(1\right)\)
Xét (O) có
\(\widehat{IMC}\) là góc tạo bởi tiếp tuyến MI và dây cung MC
Do đó: \(\widehat{IMK}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{IKM}=\widehat{IMK}\)
=>IM=IK
c: \(\widehat{IKM}=\dfrac{1}{2}\left(sđ\stackrel\frown{BM}+sđ\stackrel\frown{AC}\right)\)
\(=\dfrac{1}{2}\left(50^0+90^0\right)=70^0\)
ΔIMK cân tại I
=>\(\widehat{KIM}=180^0-2\cdot70^0=40^0\)
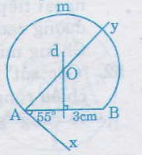
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc = 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: 
là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc \(\widehat{xAB}\)= 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)