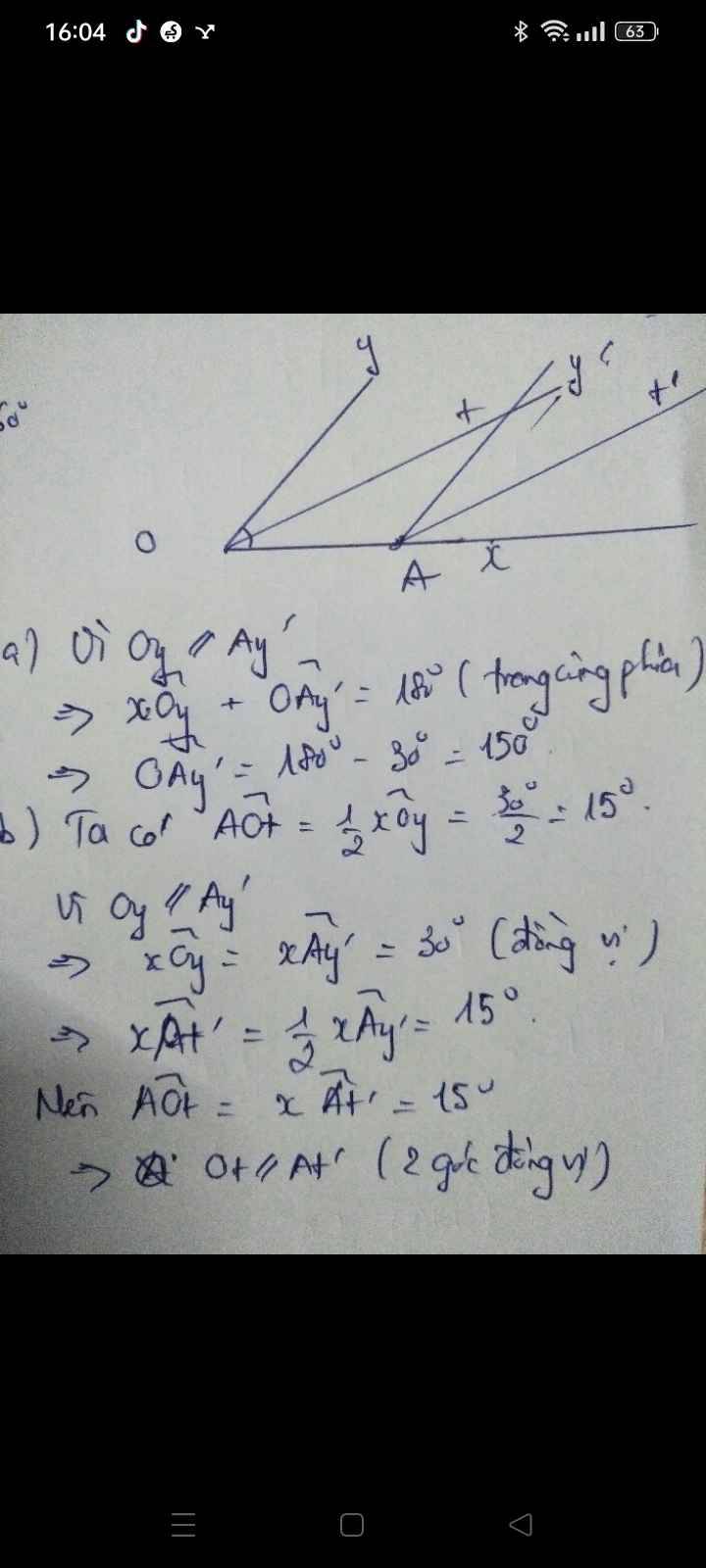Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha
a) Ví Ay' // Oy
=>\(\widehat{xAy'}=\widehat{AOy}=60độ\)
Ta có: \(\widehat{xAy'}+\widehat{OAy'}=180độ\)
\(60độ+\widehat{OAy'}=180độ\)
\(\widehat{OAy'}=120độ\)
Vậy \(\widehat{xAy'}=60độ;\widehat{OAy'}=120độ\)
b) Vì At' là tia phân giác \(\widehat{xAy'}\)
=>\(\widehat{xAt'}=\frac{\widehat{xAy'}}{2}=\frac{60độ}{2}=30độ\)
Vì Ot là tia phân giác \(\widehat{AOy}\)
=>\(\widehat{AOy}=\frac{\widehat{AOy}}{2}=\frac{60độ}{2}=30độ\)
Vậy \(\widehat{xAt'}=\widehat{AOt}=30độ\)
c) Vì \(\widehat{xAt'}=\widehat{AOt}\)
Mà 2 góc này ở vị trí đồng vị
=>Ot // At'

x O y y' t t'
a)Vì Ay' // Oy
=> ^xOy=^xAy'=60 (cặp góc đồng vị)
Có ^OAy' +^xAy'=180
=>OAy'=180- ^xAy'=180-60=120
b) Có At' là tia pg của ^xAy'
=> ^xAt' =1/2 ^xAy'=1/2 . 60=30
Tương tự cx có ^AOt=30
c)Có: ^xAt'=^AOt=30 . Mà hai góc này ở vị trí đồng vị
=> Ot//At'

a) Vì Ay′//OyAy′//Oy
→ˆxOy+ˆOAy′=180o→xOy^+OAy′^=180o (trong cùng phía bù nhau)
mà ˆxOy=30oxOy^=30o
→ˆOAy′=180o−30o=150o→OAy′^=180o−30o=150o
b) Ay′//OtAy′//Ot
→ˆxOy=ˆxAy′=30o→xOy^=xAy′^=30o (đồng vị)
OtOt là phân giác ˆxOyxOy^
→ˆxOt=ˆxOy2=30o2=15o→xOt^=xOy^2=30o2=15o
At′At′ là đường phân giác ˆxAy′xAy′^
→ˆxAt′=ˆxAy′2=30o2=15o→xAt′^=xAy′^2=30o2=15o
Từ hai điều trên →ˆxOt=ˆxẠt′=15o→xOt^=xẠt′^=15o
mà 2 góc ở vị trí đồng vị
→Ot//At′

a) Vì Ay' // Oy
=> y'AO + AOy' = 180° ( trong cùng phía)
=> y'AO = 30°
Vì Ay' // Oy
=> xAy' = AOy = 30° ( đồng vị)
b) Vì At' là phân giác xAy'
=> xAt' = t'Ay' = 30°/2 = 15°
Vì Ot là phân giác AOy
=> AOt = yOt = 30/2 = 15°
=> xAt' = AOt = 15°
Mà 2 góc này ở vị trí đồng vị
=> At' // Ot