Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{COB}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOCB
nên \(\widehat{OAD}=\widehat{OCB}\)
mà \(\widehat{MAB}=180^0-\widehat{OAD}\)
và \(\widehat{MCD}=180^0-\widehat{OCB}\)
nên \(\widehat{MAB}=\widehat{MCD}\)
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

a) ∆OAD và ∆OCB có: OA= OC(gt)
=
(=
)
OD=OB(gt)
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b) ∆OAD=∆OCB(cmt)
Suy ra: =
=
=>
=
Do đó ∆AOE = ∆OCE(c .c.c)
suy ra: =
vậy OE là tia phân giác của xOy.
b) ∆AEB= ∆CED(câu b) => EA=EC.
∆OAE và ∆OCE có: OA=OC(gt)
EA=EC(cmt)
OE là cạnh chung.
Nên ∆OAE=∆(OCE)(c .c.c)
suy ra: =
vậy OE là tia phân giác của góc xOy.

ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒  (hai góc tương ứng)
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.

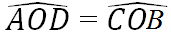
(Hình ảnh chỉ mang tính chất minh họa)
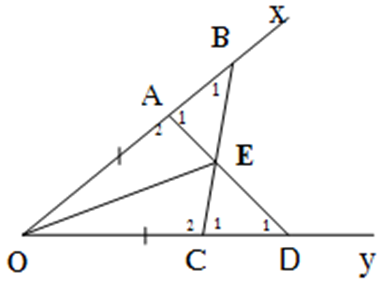
O y x C D A B M
a)* Xét \(\Delta OCB\) và \(\Delta OAD\) có:
\(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}.l\text{à}.g\text{óc}.chung\\OB=O\text{D}\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta OCB=\Delta OAD\left(c-g-c\right)\)
\(\Rightarrow AD=BC\) (hai cạnh tương ứng)
b) *Ta có: \(\Delta OCB=\Delta OAD\left(cmt\right)\)
\(\Rightarrow\) \(\widehat{B}=\widehat{D}\) (1)
*Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=O\text{D}\end{matrix}\right.\Rightarrow AB=CD\) (2)
* Ta có: \(\Delta OCB=\Delta OAD\left(cmt\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OAD}=\widehat{OCB}\\\widehat{OAD}+\widehat{DAB}=180^o\\\widehat{OCB}+\widehat{BCD}=180^o\end{matrix}\right.\)
\(\Rightarrow\widehat{DAB}=\widehat{BC\text{D}}\) (3)
*Từ (1), (2) và (3) \(\Rightarrow\Delta MAB=\Delta MCD\)
c) *Xét \(\Delta OAM\) và \(\Delta OCM\) có:
\(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\AM=CM\\OM.l\text{à.}c\text{ạnh.}chung\end{matrix}\right.\) (Vì \(\Delta MAB=\Delta MCD\Rightarrow\) 2 góc tương ứng bằng nhau)
\(\Rightarrow\Delta OAM=\Delta OCM\left(c-c-c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{AOM}=\widehat{COM}\left(2.g\text{óc.}t\text{ương.ứng}\right)\\OM.n\text{ằm}.gi\text{ữa}.OC.v\text{à.}O\text{A}\end{matrix}\right.\)
\(\Rightarrow OM\) là tia phân giác của \(\widehat{xOy}\)