Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

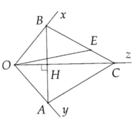
O x y z C E B A H
Xét tam giác AHO và tam giac BHO
có góc AOH = góc BOH (GT)
OH chung
góc OHA=góc OHB = 90 độ
suy ra tam giác AHO = tam giac BHO (G.C.G)
suy ra OA=OB(hai cạnh tương ứng) , HA=HB (hai cạnh tương ứng)
b) Vì góc AOB = 1000
mầ tia OH là phân giác của góc AOB
suy ra góc AOH = góc BOH =góc AOB:2=500
LẠi có OA=OB suy ra tam giác AOB cân tại O
suy ra góc ABO=góc BAO
Trong tam giác AOB có góc ABO+góc BAO +1000= 1800
suy ra góc ABO=góc BAO=400
c) Xét tam giác HBC và tam giác HAC
có BH=HA (CMT)
góc AHC=góc BHC=900
HC chung
suy ra tam giác HBC = tam giác HAC (c.g.c)
suy ra BC=CA suy ra tam giác ABC cân tại C
mà góc HBC = 600
suy ra tam giác ABC đều.
d) Xét tam giác AOB và tam giác EBO
có BE=OA=BO
góc EBO=góc AOB=1000
OB chung
suy ra tam giác AOB =tam giác EBO
suy ra AB=OE (hai cạnh tương ứng)
a)Xét hai t/g vuông OHA và OHB có:
OH(chung)
góc HOA=góc HOB(gt)
=>T/g OHA = t/g OHB(cạnh góc vuông-góc nhọn kề)
=>HA=HB;OA=OB
b)Vì OB=OA(câu a) nên t/g OAB cân tại O
=>Góc A=góc B
Do đó:
A=B=(180-O):2
=(180-100):2=40

Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)

Bạn tự vẽ hình nha!
a) Vì tia OH là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\) \(\widehat{xOH}\)=\(\widehat{yOH}\)hay \(\widehat{AOH}\)=\(\widehat{BOH}\)\((\)vì A\(\in\)Ox,B\(\in\)Oy\()\)
Xét tam giác AOH và tam giác BOH, có:
\(\widehat{AOH}\)=\(\widehat{BOH}\)
OH chung
\(\widehat{OHA}\)=\(\widehat{OHB}\)(=\(^{90^0}\))
\(\Rightarrow\)Tam giác AOH= Tam giác BOH (g-c-g)
\(\Rightarrow\)\(\hept{\begin{cases}HA=HB\\OA=OB\end{cases}}\)
Vậy....

a: Xét ΔAOC và ΔBOC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó:ΔAOC=ΔBOC
b: Ta có: ΔAOC=ΔBOC
nên CA=CB và \(\widehat{OCA}=\widehat{OCB}\)
hay CO là tia phân giác của góc BCA