

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài giải:
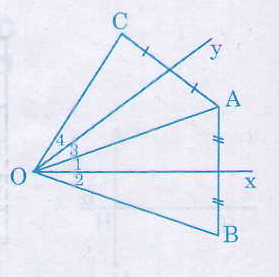
a) Ox là đường trung trực của AB nên OA = OB.
Oy là đường trung trực của AC nên OA = OC.
Suy ra OB = OC.
b) ∆AOB cân tại O (vì OA = OB).
Suy ra ˆO1O1^= ˆO2O2^= 12ˆAOB12AOB^
∆AOC cân tại O (vì OA = OC)
Suy ra ˆO3O3^= ˆO4O4^= 12ˆAOC12AOC^
Do đó ˆAOBAOB^ +ˆAOCAOC^ = 2(ˆO1O1^+ˆO3O3^)
= 2ˆxOyxOy^
= 2.500
=1000
Vậy ˆBOCBOC^ = 1000

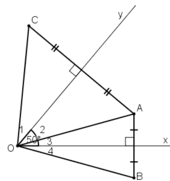
a) + B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (= OA)
b) + ΔOAC cân tại O có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
+ ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
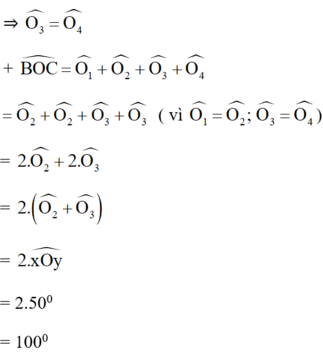

Giải :
a, Oxlaf đường trung trực của AB nên OA=OB
Oy là đường trung trực của AC nên OA=OC
=> OB=OC
b, Xét tg AOB cân tại O ( do OA=OB )
=> góc O1= góc O2 = 1/2 góc AOB
Xét tg AOC cân tại o ( vì OA=OC )
=> góc O3 = góc O4 = 1/2 góc AOC
nên góc AOB+ góc AOC= 2 (góc O1+góc O3)
= 2.góc xOy
= 2.50 độ
= 100 độ
Vậy góc BOC = 100 độ
( Hình thì dễ nên bạn tự vẽ nhé )

a; Vì C đối xứng với A qua Oy => CA vuông góc với Oy và Oy đi qua trung điểm Ca
=> O thuộc dường trung trục CA => oC = OA ( tính chất đường trung trực ) (1)
Tương tự OB = OA (2)
Từ (1) và (2) => OB = OC
b; Gọi AC giao OY tại M ; AB giao Õx tại N
OA= OB => tam giác ABO cân tại O => OM vừa là đg cao vừa là p/g => COM = AOM (1)
CMTT AON = BON
BOC = COM + AOM + AON + BON = AOM + AOM + AON + AON = 2 ( AOM + AON ) = 2. xOy = 2.50 = 100 độ