Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)xét tam giác vuông KOA và KOB có :góc KAO=góc KBO=90
OK chung
góc AOK=góc BOK
=>tam giác KAO=tam giác KBO=>KA=KB
b)xét tam giác KAD và KBE có :góc KAD=góc KBE
KA=KD
góc AKD=góc BKE
=>tam giác KAD=tam giác KBE =>KD=KE
c)có OA=OE(=OA+AD=OB+BE)=>tam giác ODE cân tại O có OK là đường phân giác=>ok đồng thời là đường cao=>OK vuông góc với DE

Trả lời:
a, ta có K là 1 điểm thuộc tia phân giác góc xOy
mà KA vuông góc với Ox và KB vuông góc với Oy (gt)
⇒ KA=KB (t/c tia phân giác của 1 góc)
b, Xét ΔOAK vuông tại A và Δ OBK vuông tại B có
OK là canh chung
góc AOK = góc BOK (gt)
⇒ 2 tam giác bằng nhau
⇒ OA = OB ( 2 cạnh tương ứng)
⇒ΔOAB cân tại O
c, Xét ΔAKD vuông tại A và Δ BKE vuông tại B
AK=BK (cmt)
góc AKD = góc BKE ( đối đỉnh)
⇒ 2 tam giác trên bằng nhau
⇒ KD = KE (đpcm)
d, ΔOAK =ΔOBK ⇒ góc OKA = góc OKB ( 2 góc tương ứng)
mà góc AKD = góc BKE ( đối đỉnh)
⇒ góc OKA + góc AKD = góc OKB + góc BKE ⇒ góc OKD = góc OKE
xét ΔOKD và OKE dễ thấy chúng bằng nhau theo th (g-c-g) ⇒ OD=OE ⇒ ΔODE cân tại O mà OK là phân giác góc DOE ⇒ OK là đường cao của DE ⇒ OK ⊥DE (đpcm)
~Học tốt!~

a: Xét ΔOAK vuông tại A và ΔOBK vuông tạiB có
OK chung
\(\widehat{AOK}=\widehat{BOK}\)
Do đó: ΔOAK=ΔOBK
Suy ra: KA=KB
b: Ta có: ΔOAK=ΔOBK
nên OA=OB
hay ΔOAB cân tại O

a) ta có: K là một điểm thuộc tia phân giác góc xOy
mà \(KA\perp Ox⋮A\)(gt)
\(KB\perp Oy⋮B\)(gt)
=> KA = KB ( tính chất tia phân giác của một góc)
b) Xét tam giác OAK vuông tại A và tam giác OBK vuông tại B
có: OK là cạnh chung
góc AOK = góc BOK ( gt)
\(\Rightarrow\Delta OAK=\Delta OBK\left(ch-gn\right)\)
=> OA = OB ( 2 cạnh tương ứng)
=> tam giác OAB cân tại O ( định lí tam giác cân)
c) Xét tam giác AKD vuông tại A và tam giác BKE vuông tại B
có: AK = BK ( phần a)
góc AKD = góc BKE ( đối đỉnh)
\(\Rightarrow\Delta AKD=\Delta BKE\left(cgv-gn\right)\)
=> KD = KE ( 2 cạnh tương ứng)
d) ta có: \(\Delta OAK=\Delta OBK\) ( chứng minh phần a)
=> góc OKA = góc OKB ( 2 góc tương ứng)
mà góc AKD = góc BKE ( đối đỉnh)
=> góc OKA + góc AKD = góc OKB + góc BKE
=> góc OKD = góc OKE
Xét tam giác \(\Delta OKD\) và \(\Delta OKE\)
có: góc KOD =góc KOE ( gt)
OK là cạnh chung
góc OKD = góc OKE ( chứng minh trên)
\(\Rightarrow\Delta OKD=\Delta OKE\left(g-c-g\right)\)
=> OD = OE ( 2 cạnh tương ứng)
=> tam giác ODE cân tại O ( định lí tam giác cân)
mà OK là tia phân giác góc DOE (gt)
=> OK là đường cao của DE ( tính chất của tam giác cân)
\(\Rightarrow OK\perp DE\) ( định lí)
mk ko bít kẻ hình trên này, sorry bn nha!
K sao đâu nhưng cx cảm ơn bn vì đã lm bài giúp mk!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

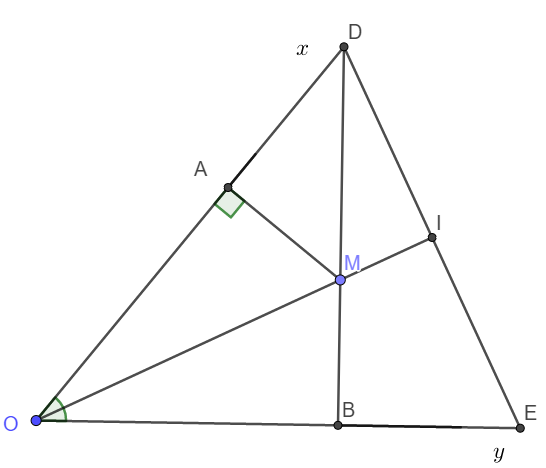
a) Xét tam giác vuông AOM và tam giác vuông BƠM có:
Cạnh huyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) (Cạnh huyền - góc nhọn)
\(\Rightarrow MA=MB;OA=AB\)hay tam giác OAB cân tại O.
b) Xét tam giác vuông AMD và tam giác vuông BME có:
AM = BM
\(\widehat{AMD}=\widehat{BME}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMD=\Delta BME\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow MD=ME\)
c) Ta thấy OA = OB; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\left(c-g-c\right)\)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.

a: Xét ΔOAN vuông tại A và ΔOBN vuông tại B có
ON chung
\(\widehat{AON}=\widehat{BON}\)
Do đó: ΔOAN=ΔOBN
Suy ra: NA=NB
b: Ta có: ΔOAN=ΔOBN
nên OA=OB
hay ΔOAB cân tại O
c: Xét ΔNAD vuông tại A và ΔNBE vuông tại B có
NA=NB
\(\widehat{AND}=\widehat{BNE}\)
Do đó: ΔNAD=ΔNBE
Suy ra: ND=NE

a,b: Xét ΔOAM vuông tại A và ΔOBM vuông tạiB co
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>OA=OB và MA=MB
=>ΔOAB cân tại O
c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
MA=MB
góc AMD=góc BME
=>ΔMAD=ΔMBE
=>MD=ME
a) Xét tam giác AKO và tam giác BKO, ta có:
Góc KAO=Góc KBO(KA vuông góc với Ox;KB vuông góc với Oy)
OK là cạnh chung
Góc AOK=Góc BOK(OK là tia phân giác góc xOy)
Suy ra: tam giác AKO=tam giác BKO
Suy ra: KA=KB(yttư)(đpcm)
và OA=OB(yttư)
b) Suy ra : tam giác OAB là tam giác cân
c) Xét tam giác AKD và tam giác BKE, ta có:
Góc KAD=Góc KBE(KA vuông góc Ox;KB vuông góc Oy)
Góc AKD=Góc BKE(2 góc đối đỉnh)
KA=KB(theo câu a)
Suy ra : tam giác AKD=tam giác BKE(g.c.g)
Suy ra: KD=KE(yttư)(đpcm)
d) Ta có : tam gíac AKD=tam giác BKE(theo câu c)
Suy ra:AD=BE(yttư)
Mà OA=OB(theo câu a)
Suy ra:OA+AD=OD=OB+BE=OE
Gọi H là giao điểm của DE và OK
Xét tam giác HOD và tam giác HOE, ta có:
OD=OE(cmt)
Góc DOH= Góc EOH(OH là tia phân giác góc DOE)
OH là cạnh chung
Suy ra:tam giác HOD=tam giác HOE(c.g.c)
Suy ra: Góc DHO=Góc EHO(yttư)
Mà đây là 2 góc kề bù
Suy ra: Góc DHO=Góc EHO=180:2=90 độ
Suy ra :OH vuông góc DE
Mà O;H;K thẳng hàng
Suy ra: OK vuông góc với DE(đpcm)