


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




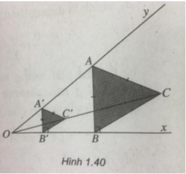
Giả sử điểm A đã dựng được . Gọi B là hình chiếu vuông góc của A trên Ox, khi đó AB = AC. Lấy điểm A' bất kì trên Oy, gọi B' là hình chiếu vuông góc của A' trên Ox, đường thẳng qua A' song song với AC cắt đường thẳng OC tại C'. Khi đó có thể coi tam giác ABC là ảnh của tam giác A'B'C' qua phép vị tự tâm O tỉ số A C A ' C ' nên A'C' = A'B'.
Từ đó suy ra cách dựng:
- Lấy điểm A bất kì trên Oy, dựng B' là hình chiếu vuông góc của A lên Ox
- Lấy C' là một giao điểm của đường tròn tâm A' bán kính A'B' với đường thẳng OC.
- Đường thẳng qua C song song với A'C' cắt Oy tại A.
Dễ thấy A là điểm phải dựng.
Bài toán có hai nghiệm hình.

- Tìm A’ đối xứng với A qua Oy , B’ đối xứng với A qua Ox
- Nối A’B’ cắt Ox tại B , cắt Oy tại C . Đó chính là hai điểm cần tìm
- Chứng minh B,C là hai điểm duy nhất cần tìm .
Thật vậy : Do A’ đối xứng với A qua Oy , cho nên CA=CA’ (1) . Mặt khác : B’ đối xứng với A qua Ox cho nên ta có BA=BB’ (2) .
Gọi P là chu vi tam giác ABC - do từ (1) và (2) - thì P=CA+CB+BA =CA’+CB+BB’=A’B’

qua O x lay D sao cho D diểm doi sung cua a qua O x lay E sao cho E ldiểm em doi sung cua a qua O y doan DE cat O x dâuau thdiểmem B ở do, DE cat O y dâuau thi C ở dó
de dang Cdượcoc tam Giác ABC có chu vi nhnhấtat

Đáp án A

Lấy A’, A” lần lượt là điểm đối xứng với A qua Ox và Oy
Tacó:
AB + AC + BC = BA’ + CA” + BC ≥ A’A” Chu vi tam giác ABC:
Dấu bằng xảy ra khi A’, A” , B , C thẳng hàng

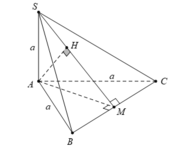
● Gọi M là trung điểm của BC ; H là hình chiếu vuông góc của A trên SM.
● Vì tam giác ABC đều nên: BC ⊥ AM.
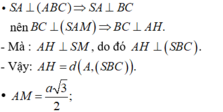
- Trong tam giác vuông SAM, đường cao AH có:

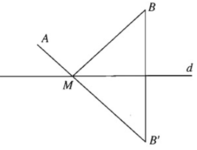
Gọi B' là ảnh của B qua phép đối xứng qua trục d.
Khi đó với mỗi điểm M thuộc d
MA + MB = MA + MB′ nên MA + MB′ bé nhất
⇔ A, M, B′ thẳng hàng.
Tức là M = (AB′) ∩ d.

Gọi H là trung điểm AD \(\Rightarrow SH\perp\left(ABCD\right)\) và \(SH=\dfrac{a\sqrt{3}}{2}\)
Gọi M là trung điểm BC \(\Rightarrow HM||CD\Rightarrow HM\perp CB\) đồng thời \(HM=CD=a\)
\(\Rightarrow BC\perp\left(SHM\right)\)
Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SBC\right)\)
\(\Rightarrow HK=d\left(H;\left(SBC\right)\right)\)
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{HM^2}\Rightarrow HK=\dfrac{SH.HM}{\sqrt{SH^2+HM^2}}=\dfrac{a\sqrt{21}}{7}\)
\(DH||BC\Rightarrow DH||\left(SBC\right)\Rightarrow d\left(D;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)=\dfrac{a\sqrt{21}}{7}\)