Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4 : * Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau. (đpcm)
Ta có hình vẽ: O A D C B E
AOBCDE
(vì kí hiệu AOC = BOD = 60o vào hình nhìn hơi rối nên mk ko kí hiệu nx nhé)
a)
- Ta có: AOC + BOC = AOB
=> 60o + BOC = 90o
=> BOC = 90o - 60o = 30o (1)
Lại có: BOC + COD = BOD
=> 30o + COD = 60o
=> COD = 60o - 30o = 30o (2)
Từ (1) và (2) => BOC = COD = 30o => OC là phân giác của BOD
- Ta có: COD + AOD = AOC
=> 30o + AOD = 60o
=> AOD = 60o - 30o = 30o
Vì COD = AOD = 30o nên OD là phân giác của AOC
b) Vì OB là phân giác của DOE nên BOD=BOE=60oBOD=BOE=60o
Ta có: BOC + BOE = COE
=> 30o + 60o = COE
=> COE = 90o
⇒OC⊥OE(đpcm)

Giải chi tiết:
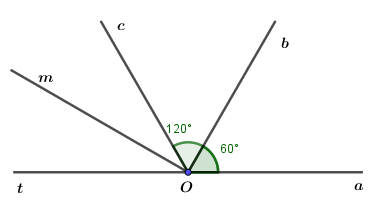
a) Trên cùng một nửa mặt phẳng bờ chứa tia OaOa, ta có ˆaOb<ˆaOc(600<1200)aOb^<aOc^(600<1200)nên ObOb là tia nằm giữa hai tia OaOa và OcOc
⇒ˆaOb+ˆbOc=ˆaOc⇒ˆbOc=ˆaOc−ˆaOb=1200−600=600⇒aOb^+bOc^=aOc^⇒bOc^=aOc^−aOb^=1200−600=600.
b) Theo chứng minh trên ta có tia ObOb là tia nằm giữa hai tia OaOa và OcOc.
Lại có ˆaOb=ˆaOc=600aOb^=aOc^=600
Suy ra ObOb là tia phân giác của ˆaOcaOc^.
c) Vì tia OtOt là tia đối của tia OaOa nên góc aOtaOt là góc bẹt, hay ˆaOt=1800aOt^=1800.
Trên cùng một nửa mặt phẳng bờ chứa tia OaOa, ta có ˆaOc<ˆaOt(1200<1800)aOc^<aOt^(1200<1800)nên OcOc là tia nằm giữa hai tia OaOa và OtOt
⇒ˆaOc+ˆcOt=ˆaOt⇒ˆcOt=ˆaOt−ˆaOc=1800−1200=600⇒aOc^+cOt^=aOt^⇒cOt^=aOt^−aOc^=1800−1200=600.
Vì OmOm là tia phân giác của ˆcOtcOt^ nên ˆcOm=12ˆcOt=6002=300cOm^=12cOt^=6002=300.
Ta có ˆbOc+ˆcOm=600+300=900bOc^+cOm^=600+300=900, do đó ˆbOcbOc^ và ˆcOmcOm^ là hai góc phụ nhau.
Chọn D

Vì:
aOb=120
aOc=70
Nên:
Ta có:aOc + bOc=aOb
Thay số:70 + bOc=120
bOc=120 - 70
bOc=50
Mà Od là tia phân giác của bOc
Suy ra:dOc=25
Vậy:
Ta có:aOc=aOc + dOc
Thay số:aOc=70 + 25
aOc=95

a, vì trên cùng nửa mặt phẳng bờ chứa tia oa có tia AOB = \(70^0\) <AOC =\(140^0\)
=> tia OB nằm giữa tia OC và OA
b, ta có BOA + BOC =COA
\(70^0\)+BOC =\(140^0\)
BOC = \(140^0-70^0\)
BOC = \(70^0\)
Vậy BOC = \(70^0\)
c, vì BOC =BOA =\(\frac{COA}{2}\)( =\(70^0\))
=>Tia OB là tia phân giác góc COA
a/Trên nửa mặt phẳng bờ chứa tia OA,ta có góc AOB= 70 độ < góc AOC= 140 độ
Vậy tia OB nằm giữa 2 tia OC và OA
b/Vì tia OB nằm giữa hai tia OC và OA nên
Ta có: góc AOB+góc BOC = góc AOC
Thay số: 70 độ + góc BOC =140 độ
Suy ra góc BOC = 140 độ - 70 độ = 70 độ
Vậy góc BOC = 70 độ
c/Tia OB là tia phân giác của góc AOC vì
+Tia OB nằm giữa hai tia OA và OC ( theo a)
+góc AOB = góc BOC = 70 độ (theo b)
d/Vì góc DOB là góc bẹt nên góc DOB = 180 độ

Ta có \(\widehat{AOD}\)+\(\widehat{BOD}\)= 180* (2 góc kề bù)
=> \(\widehat{AOD}\)+ 160* = 180*
=> \(\widehat{AOD}\)= 180* - 160* = 20*
Lại có \(\widehat{AOD}\)+\(\widehat{COD}\)=\(\widehat{AOC}\)(vì tia OD nằm giữa OA và OC)
=> 20* + \(\widehat{COD}\)= 140*
=> \(\widehat{COC}\)= 140* - 20* = 120*
- Ủng hộ -
~minhanh~

Tự vẽ hình nhé!
a, Trên cùng một nửa mặt phẳng bờ chứa tia OA ta có : AOC<AOB (50<100) nên tia Oc nằm giữa 2 tia Oa Và Ob
b, Vì tia Oc nằm giữa Oa và Ob (1)
nên ta có: aOb - aOc = cOb
100 - 50 = cOb
50 = cOb
Vậy cOb = 50 độ
Vì aOc=50 và cOb=50 nên aOc = cOb (2)
Từ (1) và (2) suy ra Oc là tia phân giác của aOb
c, ....................................................................................
Hai tia OC và OD vuông với nhau hay tạo thành 1 góc vuông là góc COD
Ta có: COD = AOB - AOC - BOD
COD = 1800 - 500 - 400 (vì góc AOB bẹt)
COD = 900
=> COD là góc vuông
Vì: AÔC = 400; AÔB = 1800
=> Tia OC nằm giữa 2 tia còn lại ( tự s2 nha )
=> AÔC + CÔB =
thui nha, chỉ viết KL thui: tia OC và OD phụ nhau