Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

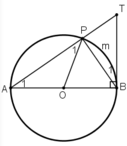

B 1 ^ l à g ó c t ạ o b ở i t i ế p t u y ế n B T v à d â y B P
⇒ B 1 ^ = 1 2 . s đ P B ⏜
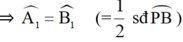
Xét tam giác APO có OA=OP=R
⇒ ∆ A P O c â n t ạ i O ⇒ A 1 ^ = P B T ^ (1)
Xét tam giác APO cân tại O ⇒ A 1 ^ = P 1 ^ (2)
Từ (1) và (2) suy ra B 1 ^ = P 1 ^ h a y A P O ^ = P B T ^

O A P T B 1 1 1 m
\(\widehat{A_1}\)là góc nội tiếp chắn cung \(\widebat{PB}\)
\(\Rightarrow\widehat{A_1}=\frac{1}{2}.sđ\widebat{PB}\)
\(\widehat{B_1}\)là góc tạo bởi tiếp tuyến BT và dây BP
\(\Rightarrow\widehat{B_1}=\frac{1}{2}.sđ\widebat{PB}\)
\(\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=\frac{1}{2}sđ\widebat{PB}\right)\)(1)
Xét \(\Delta APO\)có OA = OP = R
\(\Rightarrow\Delta APO\)cân tại O \(\Rightarrow\widehat{A_1}=\widehat{P_1}\)(2)
Từ (1) (2) => \(\widehat{B_1}=\widehat{P_1}\)hay \(\widehat{APO}=\widehat{PBT}\)


là góc tạo bởi tiếp tuyến BT và dây cung BP.
=
sđ
![]() (1)
(1)
là góc nội tiếp chắn cung
![]()
=
sđ
![]() (2)
(2)
Lại có =
(∆OAP cân) (3)
Từ (1), (2), (3), suy ra =


Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

a: Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó: ΔABC vuông tại B
Xét (O) có
ΔAFC nội tiêp
AC là đường kính
Do đó: ΔAFC vuông tại F
Xét ΔHBA vuông tại B và ΔHFC vuông tại F có
góc BHA=góc FHC
DO đó: ΔHBA đồng dạng với ΔHFC
=>HB/HF=HA/HC
=>HB*HC=HF*HA
b: Kẻ EG vuông góc với DA
Xet tứ giác EDHA có
ED//HA
EA//HD
Do đó: EDHA là hình bình hành
=>EA=DH
=>ΔEAG=ΔHDB
=>AG=BD=2AB
=>B là trung điểm của AG
=>BG=GD
=>ΔEBD cân tại E
