Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+DM=CD
nên CD=AC+BD

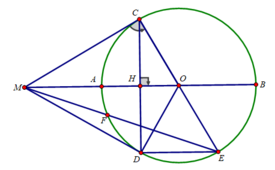
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒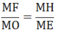
Xét ΔMOF và ΔMEN có:
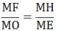
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)

a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?


a) Chứng minh rằng tứ giác ACMO nội tiếp được trong một đường tròn.
Vì AC là tiếp tuyến của (O) nên OA ⊥ AC => ˆOAC = 90o���^ = 90�
Vì MC là tiếp tuyến của (O) nên OM ⊥ MC => ˆOMC = 90o���^ = 90�
=> ˆOAC +ˆOMC =180o.���^ +���^ =180�. Suy ra OACM là tứ giác nội tiếp