Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

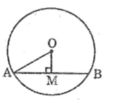
Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
O A 2 = A M 2 + O M 2
Suy ra: A M 2 = O A 2 - O M 2 = 5 2 - 3 2 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (1/2).AB
Hay: AB = 2AM = 2.4 = 8 (dm)

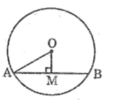
Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

O M M' A B
a) Giả sử dây AB bất kì đi qua M. Ta kẻ \(OM'\perp AB\) (M' thuộc AB)
Xét trong tam giác OMM' , ta có : \(OM\ge OM'\)(quan hệ giữa đường xiên và hình chiếu)
Do đó : dây AB dài nhất \(\Leftrightarrow AB\perp OM\)
Vậy dây ngắn nhất vuông góc với bán kính đi qua M
Tới đây áp dụng đ/l Pytago là ra...
b) Dây dài nhất là dây đi qua tâm...
O A M B
a) Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có :
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 ( dm )
Ta có: \(OM\perp AB\)
Suy ra: \(AM=\left(\frac{1}{2}\right).AB\)
Hay: AB = 2AM = 2 . 4 = 8 ( dm )
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O)
Vậy dây có độ dài bằng
2R = 2 . 5 = 10 ( dm )

Gọi dây đi qua M là AB. Kẻ OH vuông góc AB tại H.
Có MB AB≤2R=10
và OM≥OHOM≥OH quan hệ đường vuông góc và đường xiên.
vậy OH có giá trị lớn nhất bằng OM, khi đó độ dài dây AB nhỏ nhất = 8dm (liên hệ dây cung và khoảng cách đến tâm)
....... Từ đó suy ra kết quả.
a) Dây ngắn nhất đi qua M chính là dây vuông góc với bán kính.
Sau đó áp dụng đl Pytago là ra.
b) Dây dài nhất đi qua M chính là đường kính.

Gọi I là hình chiếu của O trên cạnh CD
\(\Rightarrow CI=ID=\frac{CD}{2}=\frac{18}{2}=9\left(cm\right)\)
Tam giác OCI vuông tại I
\(\Rightarrow OC=R=11\left(cm\right)\)
Mà CI = 9 ( cm )
\(\Rightarrow OI=\sqrt{40}\left(cm\right)\)
Tương tự xét tiếp cái tam giác vuông nữa rồi tính
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)