Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

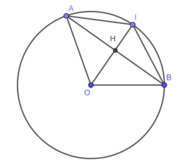
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng

Đáp án C
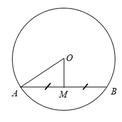
Vì M là trung điểm của AB nên ta có: 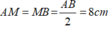
Theo quan hệ vuông góc giữa đường kính và dây ta có;
Mà khoảng cách từ O đến AM bằng 6 cm nên OM = 6 cm
Áp dụng định lí pytago vào tam giác OAM vuông ta có:
O A 2 = O M 2 + A M 2 = 6 2 + 8 2 = 100 n ê n O A = 10 c m
Suy ra: bán kính đường tròn đã cho là R = 10 cm.

Theo tc đường kính cắt dây cung thì CD⊥AB tại M
Mà M là trung điểm AB nên \(BM=\dfrac{1}{2}AB=8\)
Áp dụng PTG tam giác OBM: \(OB=\sqrt{OM^2+BM^2}=10\)

a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b; Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB

Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.
e dag can gap a