Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

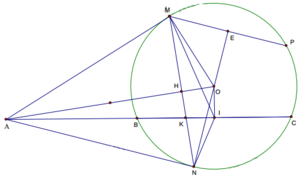
Ta có AN ⊥ NO, MP ⊥ NO, M ∉ AN => AN // MP
Do đó AMPN là hình bình hành ó AN = MP = 2x
Tam giác ∆ANO đồng dạng với ∆NEM => A N N E = N O E M = > N E = 2 x 2 R
TH 1.NE = NO – OE => 2 x 2 R = R − R 2 − x 2 ⇔ 2 x 2 = R 2 − R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 − R t ⇔ 2 t 2 − R t − R 2 = 0 ⇔ 2 t = − R t = R
Do t ≥ 0 ⇒ t = R ⇔ R 2 − x 2 = R ⇔ x = 0 ⇒ A ≡ B (loại)
TH 2 NE = NO + OE => 2 x 2 R = R + R 2 − x 2 ⇔ 2 x 2 = R 2 + R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 + R t ⇔ 2 t 2 + R t − R 2 = 0 ⇔ 2 t = R t = − R
Do t ≥ 0 ⇒ 2 t = R ⇔ 2 R 2 − x 2 = R ⇔ x = R 3 2 = > A O = 2 R (loại)
Vậy A thuộc BC, cách O một đoạn bằng 2R thì AMPN là hbh

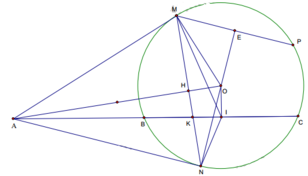
Theo giả thiết AMO = ANO = AIO = 90o = > 5 điểm A, O, M, N, I thuộc đường tròn đường kính AO 0,25
=> AIN = AMN, AIM = ANM (Góc nội tiếp cùng chắn một cung)
AM = AN => ∆AMN cân tại A => AMN = ANM
=> AIN = AIM => đpcm

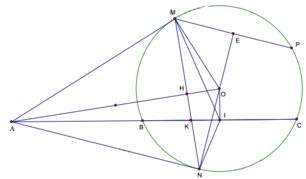
2 A K = 1 A B + 1 A C ⇔ 2 A B . A C = A K ( A B + A C ) ⇔ A B . A C = A K . A I
(Do AB+ AC = 2AI)
∆ABN đồng dạng với ∆ANC => AB.AC = AN2
∆AHK đồng dạng với ∆AIO => AK.AI = AH.AO
Tam giác ∆AMO vuông tại M có đường cao MH => AH.AO = AM2
=> AK.AI = AM2 . Do AN = AM => AB.AC = AK.AI

a, b, c HS tự làm
d, Gợi ý: G' ÎOI mà I G ' I O = 1 3 => G' thuộc (G'; 1 3 R)
