Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu c) là gì vậy, có lẽ là toán cực trị, GTLN?

a) Vì M thuộc (O) nên các tam giác BMA và CMD vuông tại M nên:
\(sin^2MBA+sin^2MAB+sin^2MCD+sin^2MDC\)
\(=\left(sin^2MBA+cos^2MBA\right)+\left(sin^2MCD+cos^2MCD\right)\)
\(=1+1=2\)
b) KOHM là hình chữ nhật nên: OK = MH
Mà MH2 = HA.HB (Hệ thức lượng trong tam giác vuông MAB có MH đường cao)
và BH = AB - AH = 2R – AH
Suy ra \(OK^2=MH^2=AH\left(2R-AH\right)\)

bn tựu vẽ hk nha
a, dễ cm tứ giác ABCD là hình thang
ta có AD//MO//CB(cùng vuông góc vs DC)
A0=B0
từ đây suy ra DM=MC
B, TỪ M KẺ MH VUÔNG GÓC VS AB
TA CÓ GÓC DAM=GÓC AMO( do AD//MO) (1)
LẠI CÓ GÓC AMO=GÓC MAO( do MO=AO) (2)
TỪ (1)(2) SUY RA GÓC DAM=GÓC MAO
LẠI CÓ GÓC D=GÓC MHA=90
SUY RA TAM GIAC DMA=TAM GIAC HMA
SUY RA AD=AH
tự BC=HB
TỪ ĐÂY SUY RA AD+CB=AH+BH=AB KO ĐỔI
C, TA CÓ MH=DM=MC(CMT)
LẠI CÓ MHVUOONG GÓC VS AB
SUY RA DƯỜNG TRÒN CD TX VS AB
D, TRONG HT VUÔNG ABCD CÓ DC<=AB
SUY RA SABCD=\(\frac{\left(AD+CB\right).DC}{2}=\frac{AB.CD}{2}< =\frac{AB^2}{2}\)
DẤU = XẢY RA KHI M NẰM CHÍNH GIỬA CUNG AB

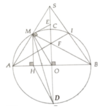
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC
Do tính đối xứng, không mất tính tổng quát, giả sử M nằm trên cung nhỏ AC
Từ M lần lượt kẻ ME vuông góc AB và MF vuông góc CD
Do \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{AMB}=90^0\) hay tam giác AMB vuông tại M
Áp dụng hệ thức lượng: \(ME.AB=MA.MB\) \(\Leftrightarrow MA.MB=2R.ME\)
Tương tự: \(MC.MD=2R.MF\)
\(\Rightarrow MA.MB.MC.MD=4R^2.ME.MF\)
\(\Rightarrow\) Tích số đã cho đạt max khi \(ME.MF\) đạt max
Lại có tứ giác MEOF là hình chữ nhật (4 góc vuông)
\(\Rightarrow EF=MO=R\)
Áp dụng BĐT \(ab\le\dfrac{1}{2}\left(a^2+b^2\right)\) ta có:
\(ME.MF\le\dfrac{1}{2}\left(ME^2+MF^2\right)=\dfrac{1}{2}EF^2=\dfrac{1}{2}R^2\)
Dấu "=" xảy ra khi và chỉ khi \(ME=MF\) hay M nằm chính giữa cung AC
Vậy MA.MB.MC.MD đạt max khi M nằm chính giữa một trong các cung nhỏ AC, CB, BD hoặc DA