Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O B A C E
Vì tam giác ABC cân tại A nên \(\widehat{ACB}=\widehat{ABC}\)
Lại có \(\widehat{ACB}\) và \(\widehat{OCE}\) là hai góc đối đỉnh nên chúng bằng nhau. Nói cách khác \(\widehat{OCE}=\widehat{ABC}\)
Do OE = OB nên \(\widehat{OEB}=\widehat{OBE}\)
Mà \(\widehat{ABC}+\widehat{OBE}=90^o\Rightarrow\widehat{OCE}+\widehat{OEB}=90^o\Rightarrow\widehat{EOC}=90^o.\)
Vậy \(OE\perp OA.\)

a: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC nên OH là phân giác của góc BOC
OH*OA=OB^2=R^2
b: Xét ΔOBA và ΔOCA có
OB=OC
góc BOA=góc COA
OA chung
Do đo: ΔOBA=ΔOCA
=>góc OCA=90 độ
=>AC là tiếp tuyến của (O)

a: Gọi H là trung điểm của OA
Xét (O) có
OH là một phần đường kính
BC là dây
OH⊥BC tại H
Do đó: H là trung điểm của BC
Xét tứ giác ABOC có
H là trung điểm của đường chéo AO
H là trung điểm của đường chéo BC
Do đó: ABOC là hình bình hành
mà OB=OC
nên ABOC là hình thoi

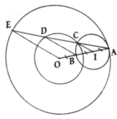
a, Gọi I là trung điểm của AB, ta có: OI = OA – IA
b, Ta chứng minh được IC//BD//OE
Mà OB = BI = IA => AC = CD = DE

Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng i: Đoạn thẳng [A, B] Đoạn thẳng j: Đoạn thẳng [A, C] Đoạn thẳng k: Đoạn thẳng [O, B] Đoạn thẳng l: Đoạn thẳng [O, C] Đoạn thẳng m_1: Đoạn thẳng [B, C] Đoạn thẳng n: Đoạn thẳng [O, A] Đoạn thẳng m: Đoạn thẳng [M, E] Đoạn thẳng q: Đoạn thẳng [F, M] Đoạn thẳng s: Đoạn thẳng [E, E'] Đoạn thẳng t: Đoạn thẳng [E', M] Đoạn thẳng a: Đoạn thẳng [F, E] O = (0.7, 2.54) O = (0.7, 2.54) O = (0.7, 2.54) Điểm A: Giao điểm đường của d, f Điểm A: Giao điểm đường của d, f Điểm A: Giao điểm đường của d, f Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm M: Giao điểm đường của m_1, n Điểm M: Giao điểm đường của m_1, n Điểm M: Giao điểm đường của m_1, n Điểm E: Điểm trên i Điểm E: Điểm trên i Điểm E: Điểm trên i Điểm F: Giao điểm đường của p, j Điểm F: Giao điểm đường của p, j Điểm F: Giao điểm đường của p, j Điểm E': Giao điểm đường của r, j Điểm E': Giao điểm đường của r, j Điểm E': Giao điểm đường của r, j
Do OA = 2R nên xét tam giác vuông OBA có \(sin\widehat{BAO}=\frac{1}{2}\Rightarrow\widehat{BAO}=30^o\Rightarrow\widehat{BAC}=60^o\)
Theo tính chất tiếp tuyến, ta có AB = AC.
Vậy thì tam giác ABC đều. Từ đó \(\widehat{EMF}=\widehat{BAC}=60^o.\)
Trên AC lấy điểm E' sao cho BE = CE'.
Do tam giác ABC đều nên ta có ngay \(\Delta BEM=\Delta CE'M\left(c-g-c\right)\Rightarrow\widehat{BME}=\widehat{CME'}\) (1)
Cũng do tam giác ABC đều nên AB = AC. Lại có BE = CE' nên EE' // BC.
Từ đó ta có \(\widehat{CME'}=\widehat{EE'M}\) (2)
Do EE' // BC nên \(\widehat{EE'A}=\widehat{BCA}=60^o\) (Hai góc đồng vị)
Xét tứ giác EFE'M có \(\widehat{EMF}=\widehat{EE'A}\left(=60^o\right)\) nên nó là tứ giác nội tiếp.
Vậy ta suy ra \(\widehat{EE'M}=\widehat{EFM}\) (Hai góc nội tiếp cùng chắn một cung) (3)
Từ (1), (2), (3) ta có \(\widehat{BME}=\widehat{CME'}=\widehat{EE'M}=\widehat{EFM}\Rightarrow\widehat{BME}=\widehat{EFM}\)
Xét tam giác BEM và tam giác MEF có \(\widehat{EBM}=\widehat{EMF}=60^o\) và \(\widehat{BME}=\widehat{MFE}\)
Vậy thì \(\Delta BEM\sim\Delta MEF\left(g-g\right)\Rightarrow\widehat{BEM}=\widehat{MEF}\) hay EM là tia phân giác của góc BEF.
Tham khảo đi Akashiya Moka
bạn hãy vẽ hình ra nhá.
Gọi I là giao của OA và (O;R) ,Tam giác OBI đều do OI = BI = BO = R ( Do tam giác vuông ABO có OA = 2R suy ra OI bằng R và BI là trung tuyến nên = 1 nửa cạnh huyền OA và = R nốt )
vậy góc BOA bằng 60 vậy góc BAO bằng 30 và BAC bang 60 ( do OA pân giác BAC ) vậy tam giác BAC cân tại A có A bằng 60 suy đều
Có góc BOA bằng 60 suy ra góc AOS bằng 30 ( vì BOS là góc 90 ) mặ khác ÁO bằng 30 suy tam giác ÁO cân tại S