Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH là đường trung trực của AB(1)
Ta có: IA=IB
nên I nằm trên đường trung trực của AB(2)
từ (1), (2) suy ra O,H,I thẳng hàng
b: Vì I là điểm chính giữa của cung CD nên IC=ID
mà OC=OD
nên OI là đường trung trực của CD
=>CD//AB hoặc CD trùng với AB

Vì I là điểm chính giữa của cung AB nên IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,I thẳng hàng

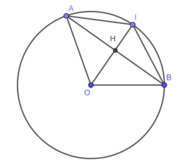
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng

OB=OC
MB=MC
=>OM là trung trực của BC
=>OM vuông góc BC tại I
góc CHO+góc CIO=180 độ
=>CHOI nội tiếp