Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

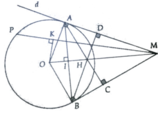
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng

1) ta có :\(\left\{{}\begin{matrix}MA\perp OA\\MB\perp OB\end{matrix}\right.=>}\widehat{MAO}=90;\widehat{MBO}=90\)
=> tứ giác AMBO nội tiếp
a) ta có
MA ; MB là các tiếp tuyến của (O)
⇒gócMAO=90 ; MBO = 90
⇒tú giác AMBO nội tiếp

a: ΔONP cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)NP tại K
Ta có: \(\widehat{OAM}=\widehat{OBM}=\widehat{OKM}=90^0\)
=>O,A,M,B,K cùng thuộc đường tròn đường kính OM
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot OM=OA^2=R^2\)
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot IM=IA^2\)
c: AC\(\perp\)BM
OB\(\perp\)BM
Do đó: OB//AC
=>OB//AH
BD\(\perp\)MA
OA\(\perp\)MA
Do đó: BD//OA
=>BH//OA
Xét tứ giác OBHA có
OB//HA
OA//HB
Do đó: OBHA là hình bình hành
Hình bình hành OBHA có OB=OA
nên OBHA là hình thoi
d: OBHA là hình thoi
=>OH là đường trung trực của BA
mà M nằm trên đường trung trực của BA(cmt)
nên O,H,M thẳng hàng

1 vì K là trung điểm NP nên OK vuông góc NP ( Quan hệ đường kính và dây cung ) suy ra góc OKM=90 độ .Theo tính chất tiếp tuyến ta có góc OAM=90 độ , góc OBM = 90 độ như vậy K,A,B cùng nhìn OM dưới một góc 90 độ nên cùng nằm trên dường tròn đường kính OM . vậy ..........