Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

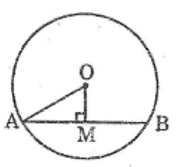
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

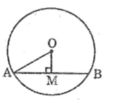
Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
O A 2 = A M 2 + O M 2
Suy ra: A M 2 = O A 2 - O M 2 = 5 2 - 3 2 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (1/2).AB
Hay: AB = 2AM = 2.4 = 8 (dm)

a,b: Xét (O) có
AE,AH là tiếp tuyến
=>AE=AH và OA là phân giác của góc EOH
AE=AH
OE=OH
Do đó:OA là trung trực của EH
=>OA vuông góc EH tại M và M là trung điểm của EH
ΔEMO vuông tại M
=>MO^2+ME^2=OE^2
=>ME^2=5^2-3^2=16
=>ME=4(cm)
=>MH=2*4=8cm
Xét ΔOEA vuông tại E có EM là đường cao
nên OE^2=OM*OA
=>OA=5^2/3=25/3(cm)
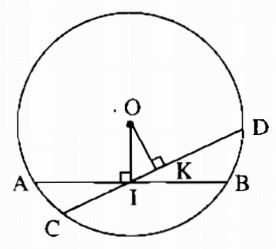
c: ΔOEK cân tại O
mà OB là trung tuyến
nên OB vuông góc KE tại I và OB là phân giác của góc KOE
Xét ΔOKB và ΔOEB có
OK=OE
góc KOB=góc EOB
OB chung
Do đó: ΔOKB=ΔOEB
=>góc OBK=góc OEB=90 độ
=>BK là tiếp tuyến của (O)
d: Xét (O) có
ΔKEH nội tiếp
KH là đường kính
Do đó: ΔKEH vuông tại E
Xét tứ giác OIEM có
góc IEM=góc EIO=góc IOM=90 độ
=>OIEM là hình chữ nhật


a, 2πR = 4π => R = 2cm
b, A O B ^ = 60 0 (DOAB đều)
=> B O C ^ = 120 0
l B C ⏜ n h ỏ = π . R . 120 180 = 4 π 3 cm
và l B C ⏜ l ớ n = 8 3 π cm