Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

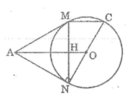
Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
A O 2 = A N 2 + O N 2
Suy ra : A N 2 = A O 2 - O N 2 = 5 2 - 3 2 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
Xét ΔOAM vuông tại A có \(tanAOM=\dfrac{AM}{OA}\)
=>\(\dfrac{AM}{9}=tan30=\dfrac{1}{\sqrt{3}}\)
=>\(AM=\dfrac{9}{\sqrt{3}}=3\sqrt{3}\left(cm\right)\)