Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi x=-2 thì (y+2)^2=25-(-2-1)^2=25-9=16
=>y=2 hoặc y=-6
TH1: A(-2;2)
I(1;-2)
vecto IA=(-3;4)
Phương trình Δ là:
-3(x-1)+4(y+2)=0
=>-3x+3+4y+8=0
=>-3x+4y+11=0
TH2: A(-2;-6); I(1;-2)
vecto IA=(-3;-4)=(3;4)
Phương trình IA là:
3(x+2)+4(y+6)=0
=>3x+6+4y+24=0
=>3x+4y+30=0
b: Δ//12x+5y+6=0
=>Δ: 12x+5y+c=0
d(I;Δ)=5
=>\(\dfrac{\left|12\cdot1+5\cdot\left(-2\right)+c\right|}{\sqrt{12^2+5^2}}=5\)
=>|c+2|=5*13=65
=>c=63 hoặc c=-67

a) Khoảng cách từ điểm A đến đường thẳng \(\Delta \) là: \(d\left( {A,\Delta } \right) = \frac{{\left| {0 - 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 3\sqrt 2 \).
b) Ta có: \(\overrightarrow {{n_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\). Phương trình đường thẳng a là:
\(1\left( {x + 1} \right) + 1\left( {y - 0} \right) = 0 \Leftrightarrow x + y + 1 = 0\)
c) Ta có: \(\overrightarrow {{u_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\).Từ đó suy ra \(\overrightarrow {{n_b}} = \left( {1; - 1} \right)\). Phương trình đường thẳng b là:
\(1\left( {x - 0} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow x - y + 3 = 0\)

Gọi \(M\left( {x;y} \right)\)
Ta có: \(\overrightarrow {AM} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow n = \left( {a;b} \right)\)
\( M \in \Delta \Leftrightarrow \overrightarrow {AM} \bot \overrightarrow n \)
Hay \(\overrightarrow {AM} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0\) (ĐPCM).

a) \(\Delta \) song song với đường thẳng \(3x + y + 9 = 0\) nên nhận vectơ pháp tuyến của đường thẳng này làm vectơ pháp tuyến là \(\overrightarrow n = \left( {3;1} \right)\)
\(\Delta \) đi qua điểm \(A(2;1)\) nên ta có phương trình tổng quát
\(3\left( {x - 2} \right) + \left( {y - 1} \right) = 0 \Leftrightarrow 3x + y - 7 = 0\)
\(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;1} \right)\) nên có vectơ chỉ phương là \(\overrightarrow u = \left( {1; - 3} \right)\)
Phương trình tham số của đường thẳng \(\Delta \) là:
\(\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 3t\end{array} \right.\)
b) \(\Delta \) vuông góc với đường thẳng \(2x - y - 2 = 0\) nên nhận vectơ pháp tuyến của đường thẳng này làm vectơ chỉ phương là \(\overrightarrow u = \left( {2; - 1} \right)\)
\(\Delta \) đi qua điểm \(B( - 1;4)\) nên ta có phương trình tham số: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 4 - t\end{array} \right.\)
\(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 1} \right)\) nên có vectơ pháp tuyến là \(\overrightarrow n = \left( {1;2} \right)\)
Phương trình tổng quát của đường thẳng \(\Delta \)là:
\(\left( {x + 1} \right) + 2\left( {y - 4} \right) = 0 \Leftrightarrow x + 2y - 7 = 0\)

a) Nếu b = 0 và \(a \ne 0\) thì phương trình đường thẳng \(\Delta \) trở thành \(ax + c = 0\) . Khi đó đường thẳng \(\Delta \) song song hoặc trùng với trục \(Oy\) và cắt trục \({\rm{O}}x\) tại điểm \(\left( { - \frac{c}{a};0} \right)\).
b) \(b \ne 0\) và a = 0 thì phương trình đường thẳng \(\Delta \) trở thành \(by + c = 0\) . Khi đó đường thẳng \(\Delta \) song song hoặc trùng với trục \({\rm{O}}x\) và cắt trục \(Oy\) tại điểm \(\left( {0; - \frac{c}{b}} \right)\).
c) Nếu \(b \ne 0\) và \(a \ne 0\)thì phương trình đường thẳng \(\Delta \) có thể viết thành \(y = - \frac{a}{b}x - \frac{c}{b}\). Khi đó, đường thẳng \(\Delta \) là đồ thị hàm số bậc nhất \(y = - \frac{a}{b}x - \frac{c}{b}\)vời hệ số góc là \(k = - \frac{a}{b}\).

a: Vì Δ//d nên Δ: 3x-4y+c=0
Thay x=1 và y=4 vào Δ, ta được:
c+3-16=0
=>c=13
b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0
Thay x=-3 và y=-5 vào Δ, ta được:
c+4*(-3)+3(-5)=0
=>c-27=0
=>c=27
=>4x+3y+27=0

a.
Gọi \(M\left(x;y\right)\in d\)
\(\Rightarrow d\left(M;\Delta\right)=3\Leftrightarrow\dfrac{\left|3x-4y+6\right|}{\sqrt{3^2+4^2}}=3\)
\(\Leftrightarrow\left|3x-4y+6\right|=15\Rightarrow\left[{}\begin{matrix}3x-4y+21=0\\3x-4y-9=0\end{matrix}\right.\)
b.
Giả sử đường thẳng (d2) có dạng \(a\left(x+2\right)+b\left(y-3\right)=0\Leftrightarrow ax+by+2a-3b=0\) (1)
\(\dfrac{\left|3.a-4b\right|}{5\sqrt{a^2+b^2}}=\dfrac{1}{\sqrt{2}}\Leftrightarrow2\left(3a-4b\right)^2=25a^2+25b^2\)
\(\Leftrightarrow7a^2+48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}7a=b\\a=-7b\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(1;7\right);\left(7;-1\right)\)
\(\Rightarrow...\) (bạn tự thế vào (1) và rút gọn)

Tham khảo:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
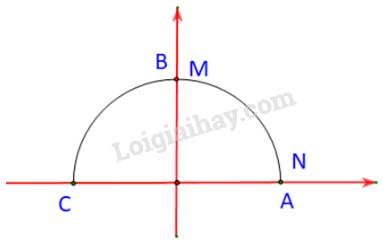
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
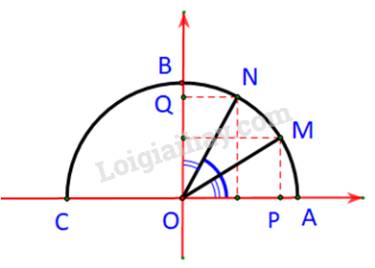
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)

a, Phương trình đường thẳng song song với \(\Delta\) và đi qua \(M\left(1;\dfrac{1}{2}\right)\) là \(y=\dfrac{1}{2}\)
b, Phương trình đường thẳng vuông góc với \(\Delta\) và đi qua \(M\left(3;4\right)\) là \(x=3\)
c, Phương trình đường thẳng vuông góc với \(\Delta\) và đi qua \(M\left(-1;2\right)\) là \(y=2\)
a) Xét hệ phương trình: \(\left\{ \begin{array}{l}y = 0\\y = ax + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = \frac{{ - b}}{a}\end{array} \right.\) . Vậy đường thẳng \(\Delta \) cắt trục hoành tại điểm \(\left( {\frac{{ - b}}{a};0} \right)\).
b) Phương trình đường thẳng \({\Delta _o}\) đi qua O(0, 0) và song song (hoặc trùng) với\(\Delta \) là \(y = a\left( {x - 0} \right) + 0 = {\rm{a}}x\).
c) Ta có: \({\alpha _\Delta } = {\alpha _{{\Delta _o}}}\).
d) Từ câu b) và điều kiện \(x_o^2 + y_o^2 = 1\) trong đó \({y_o}\) là tung độ của điểm M, ta suy ra \({x_o} \ne 0\). Do đó: \(\tan {\alpha _\Delta } = \tan {\alpha _{{\Delta _o}}} = \frac{{{y_o}}}{{{x_o}}} = a\).