Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

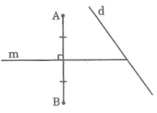
* Nếu AB không vuông góc với d
- Vì điểm C cách đều hai điểm A và B nên C nằm trên đường trung trực của AB.
- Điểm C ∈ d
Vậy C là giao điểm của đường trung trực của AB và đường thẳng d.
Cần dựng đường thẳng m là đường trung trực của đoạn thẳng AB cắt đường thẳng d tại C.
Vậy C là điểm cần tìm.
* Nếu AB vuông góc với d
Khi đó đường trung trực của AB song song với đường thẳng d nên không tồn tại điểm C.

Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)

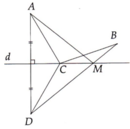
Lấy D là điểm đối xứng, với A qua d. Theo tính chất đường trung trực: CA = CD.
Do đó CA + CB = CD + CB.
Gọi M là giao điểm của BD và d.
Nếu C không trùng với M thì xét tam giác BCD, ta có: CB + CD > BD hay CA + CB > BD (1).
Nếu C trùng với M thì:
CA + CB = MA + MB = MD + MB = BD (2).
So sánh (1) và (2) ta thấy điểm C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB là nhỏ nhất.
Chú ý: Điểm C tìm được ở vị trí M như vậy là điểm duy nhất. Thật vậy, nếu lấy E đối xứng với B qua d thì AE vẫn cắt d ở M đúng vị trí mà BD cắt d.

Điểm C phải đường thẳng trung trực của AB
cách vẽ
Từ M trung điểm AB
cách xác định Điểm M
(1)dùng com pa lấy A làm tâm bán kinh R>1/2AB vẽ cung nhỏ cắt AB
(2)dùng com pa lấy B làm tâm bán kinh R >1/2AB vẽ cung nhỏ cắt AB
Cung (1) cắt cung (2) tại hai điểm "lý do R>1/2AB là vây)
Nối hai điểm này => M
Kéo dài => cắt (d) đó chính là Điểm C cần tìm
C cách đều A và B khi CA=CB