Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
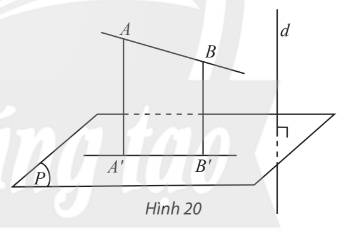
\(\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
b) Ta có:
\(\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).

a) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)\)

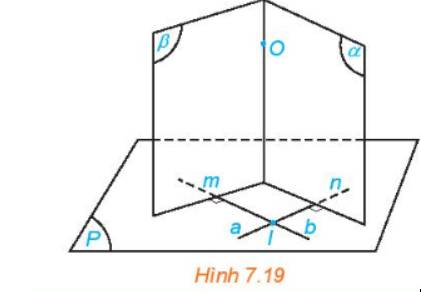
a) Vì \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và giao 2 mặt phẳng là 1 đường thẳng nên hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng đi qua O.
b) Gọi \(\Delta \) là giao tuyến của 2 \(\left( \alpha \right),\left( \beta \right)\)
\(\left. \begin{array}{l}a \bot \left( \alpha \right)\\\Delta \subset \left( \alpha \right)\end{array} \right\} \Rightarrow a \bot \Delta \)
\(\left. \begin{array}{l}b \bot \left( \beta \right)\\\Delta \subset \left( \beta \right)\end{array} \right\} \Rightarrow b \bot \Delta \)
Mà \(a \cap b = \left\{ I \right\} \Rightarrow \Delta \bot \left( P \right)\)

S A B C D H O K I L T
a) SA vuông góc với (ABCD) => SA vuông góc AD; hình thang ABCD vuông tại A => AD vuông góc AB
=> AD vuông góc (SAB), mà AD nằm trong (SAD) nên (SAB) vuông góc (SAD).
b) AD vuông góc (SAB), BC || AD => BC vuông góc (SAB) => B là hc vuông góc của C trên (SAB)
=> (SC,SAB) = ^CAB
\(SB=\sqrt{AS^2+AB^2}=\sqrt{2a^2+a^2}\)\(=a\sqrt{3}\)
\(\tan\widehat{CAB}=\frac{BC}{SB}=\frac{a}{a\sqrt{3}}=\frac{\sqrt{3}}{3}\)=> (SC,SAB) = ^CAB = 300.
c) T là trung điểm của AD, K thuộc ST sao cho AK vuông góc ST, BT cắt AC tại O, HK cắt AO tại I, AI cắt SC tại L.
BC vuông góc (SAB) => BC vuông góc AH, vì AH vuông góc SB nên AH vuông góc SC. Tương tự AK vuông góc SC
=> SC vuông góc (HAK) => SC vuông góc AI,AL. Lập luận tương tự thì AL,AI vuông góc (SCD).
Dễ thấy \(\Delta\)SAB = \(\Delta\)SAT, chúng có đường cao tương ứng AH và AK => \(\frac{HS}{HB}=\frac{KS}{KT}\)=> HK || BT || CD
=> d(H,SCD) = d(I,SCD) = IL (vì A,I,L vuông góc (SCD)) = \(\frac{IL}{AL}.AL=\frac{CO}{CA}.\frac{SI}{SO}.AL=\frac{1}{2}.\frac{SH}{SB}.\frac{AS.AC}{\sqrt{AS^2+AC^2}}\)
\(=\frac{1}{2}.\frac{SA^2}{SA^2+SB^2}.\frac{AS.AC}{\sqrt{AS^2+AC^2}}=\frac{1}{2}.\frac{2a^2}{2a^2+a^2}.\frac{a\sqrt{2}.a\sqrt{2}}{\sqrt{2a^2+2a^2}}=\frac{a}{3}\)

tham khảo:
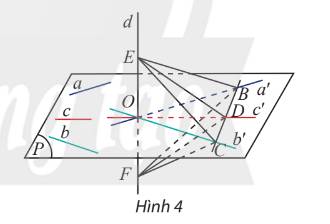
a) Vì a//a', d⊥a nên d⊥a′, Hay EF⊥OB
Tam giác EBF có OB⊥EF; O là trung điểm EF nên tam giác EBF cân tại B. Suy ra BE = BF
Tương tự ta chứng minh được CE = CF
Suy ra tam giác CEB bằng tam giác CFB
b) Vì tam giác CEB và CFB bằng nhau nên DE = DF
Nên tam giác DEF cân tại D có DO là trung tuyến nên DO⊥EF
Suy ra d⊥c

Gọi (R) là mặt phẳng chứa a và (R)//(Q)
(Q)//(R)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(\left(P\right)\cap\left(R\right)=a\)
Do đó: a//a'
mà IJ vuông góc a
nên JI vuông góc a'
\(\left(P\right)\perp\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(JI\perp a\)
Do đó: JI vuông góc (Q)
=>IJ vuông góc b
tham khảo:
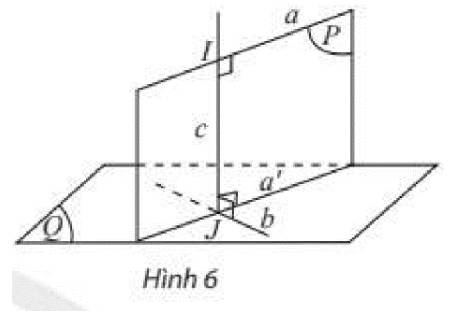
Gọi (R) là mặt phẳng chứa a song song với (Q).
(P) cắt hai mặt phẳng song song tại a và a' nên a//a'
Trong mặt phẳng (P), IJ⊥a,a//a′ nên IJ⊥a′
Ta có: (P)⊥(Q), (P) cắt (Q) tại a', IJ⊥a′ nên IJ⊥(P)
Suy ra IJ⊥b





THAM KHẢO
a) Nếu a⊥(P) thì a vuông góc với mọi đường thẳng thuộc (P)
Góc giữa a và một đường thẳng b tuỳ ý trong (P) là \(90^0\)
b) (a,a′)=α