Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

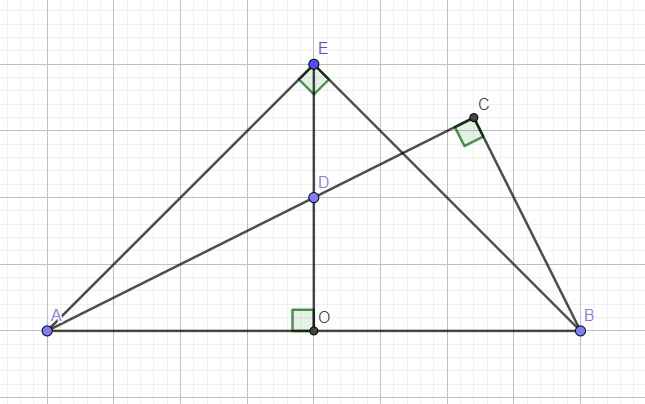
O là trung điểm AB \(\Rightarrow OA=OB=\dfrac{AB}{2}=a\)
Áp dụng định lý Pitago:
\(AD=\sqrt{AO^2+OD^2}=\dfrac{a\sqrt{5}}{2}\)
Xét hai tam giác vuông AOD và ACB có góc A chung
\(\Rightarrow\Delta AOD\sim\Delta ACB\Rightarrow\dfrac{AD}{AB}=\dfrac{AO}{AC}\Rightarrow AC=\dfrac{AO.AB}{AD}=\dfrac{4a\sqrt{5}}{5}\)
\(BC=\sqrt{AB^2-AC^2}=\dfrac{2a\sqrt{5}}{5}\)
b. Ta có: \(AE=\sqrt{AO^2+OE^2}=a\sqrt{2}\)
\(BE=\sqrt{OB^2+OE^2}=a\sqrt{2}\)
\(\Rightarrow AE^2+BE^2=4a^2=AB^2\)
\(\Rightarrow\Delta ABE\) vuông tại E (Pitago đảo)
\(\Rightarrow\) Hai điểm E và C cùng nhìn AB dưới 1 góc vuông nên bốn điểm A,B,C,E cùng thuộc đường tròn đường kính AB (đpcm)

b: Xét (O) có
OH là một phần đường kính
AD là dây
OH\(\perp\)AD tại H
Do đó: H là trung điểm của AD
Suy ra: \(AH\cdot HD=AH^2\left(1\right)\)
Xét (O) có
ΔBAC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot HC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot HD=HB\cdot HC\)

a) ta có AO=BO=OC=R=(BC/2)
=> tam giác ABC vuông tại A(t/c đường trung tuyến trg tam giác vuông)
=>AC=\(\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=\sqrt{100-36}=8\)
Xét tam giác CBD vuông tại B có đường cao BA
=> \(BC^2=AC.CD\)
=> CD=\(\dfrac{BC^2}{AC}=\dfrac{100}{8}=\dfrac{25}{2}=12,5\left(Cm\right)\)
b) câu b bn chưa cho cm cái j hết nhm theo mik chắc là cm DE.DO=AD.CD
Xét tam giác BDO vuông tại B có đường cao BE
=> AB(^2)=DE.DO(1)
Xét tam giác BCD vuông tại B có đường cao AB
=>AB(^2)=AD.CD(2)
Từ (1) và (2) => DE.DO=AD.CD