Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

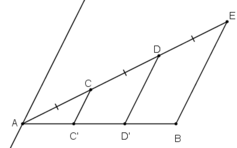
Kẻ đường thẳng At // CC’ // DD’ // BE như hình vẽ.
Ta có: AC = CD = DE
⇒ At, CC’, DD‘, BE là các đường thẳng song song cách đều
⇒ AC’ = C’D’ = D’B
hay đoạn thẳng AB bị chia ra làm 3 phần bằng nhau.

Ta có AC = CD và CC’ // BE
CD = DE và DD’ // BE
=> CC’ // DD’ và CEBC’ là hình thang
=> CC’ là đường trung bình của tam giác ADD’
DD’ là đường trung bình của hình thang CEBC’
=> AC’ = CD’ và C’D’ = D’B => AC’ = CD’ = D’B

Bài giải:
Ta có: EB // DD' // CC' và AE = CD = DE.
Nên theo định lí về các đường thẳng song song cách đều ta suy ra
AC' = C'D' = D'B
Vậy đoạn thẳng AB bị chia ra ba phần bằng nhau.
Xét tứ giác C'CEB có: CC'//EB (gt)
=> C'CEB là hình thang
Xét \(\Delta\)ADD' có : AC=CD (gt)
CC'=Đ' (gt)
=>AC'=C'D' (định lí 1) (1)
Xét hình thang CC'EB có: CD=DE (gt)
DD'//EB
=>C'D'=D'B(định lí 1) (2)
Từ (1) và (2) =>AC'=C'D'=D'B
Vậy đoạn thẳng AB được chia thành 3 phần bằng nhau.


Xét tam giác \(ADD_1\) có AC=DC(gt); \(CC_1\text{//}DD_1\) ta có:
\(AC_1=D_1C_1\) (theo tính chất của đường trung bình của tam giác)
Xét hình thang \(CEBC_1\) có CD=ED(gt); \(DD_1\text{//}BE\) ta có:
\(C_1D_1=BD_1\) (theo tính chất của đường trung bình của hình thang)
Do đó \(AC_1=C_1D_1=D_1B\) (đpcm)
Chúc bạn học tốt!!! (bạn sửa hết \(C_1;D_1\) thành C'; D' hộ mình nha!)
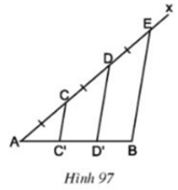

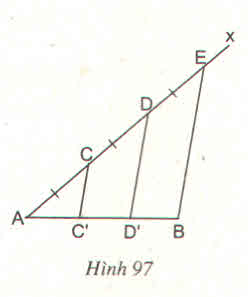
Xét tam giác ADD' , có :
. C trung điểm AD ( AC = CD ; C thuộc AD )
. CC' // DD' ( // BE )
. C' thuộc AD' ( CC' cắt AD' tại C' )
Suy ra : C' là trung điểm AD'
=> AC' = C'D' ( 1 )
Xét hình thang CC'BE ( CC' // BE ) , có :
. D' là trung điểm BC'
. DD' // BE // CC' ( cmt )
. D' thuộc BC'( DD' cắt BC' tại D' )
Suy ra : D' là trung điểm BC'
=> BD' = C'D' ( 2 )
Từ ( 1 ) và ( 2 ) , cho : AC' = C'D' = D'B
cho mình xin cái hình m.n ơi