Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo t/c 2 tiếp tuyến cắt nhau, ta có
góc AOC = góc COM
góc MOD = góc DOB
=> COM +MOD =AOC +BOD = 1/2 AOB = 90o (đpcm)
b) Xét tam giác AOC và tg BDO
Có góc AOC = góc BDO ( cùng phụ BOD)'
góc ACO = góc BOD ( cùng phụ AOC )
=> tg AOC đồng dạng tg BDO (gg)
=> \(\frac{AC}{AO}=\frac{BO}{BD}\Rightarrow AC.BD=AO.BO=R^2\)

d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm

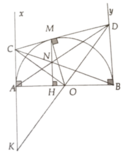
a, Kẻ OM ⊥ CD
Gọi K = OD ∩ d => ∆COK = ∆COD
=> OK = OD => OM = OA = R => CD là tiếp tuyến
b, AC+BD=CM+DM=CD ≥ AB
Do đó min (AC+BD)=AB
<=> CD//AB => ABCD là hình chữ nhật <=> AC = AO
c, AC.BD = MC.MD = O M 2 = 4 a 2
=> 1 O C 2 + 1 O D 2 = 1 4 a 2
d, Từ tính chất hai giao tuyến => MN//BD => MNAB hay MHAB;
AC//BD; MN//BD; NH//BD
=> M N B D = N H B D => MN = NH
hình ông tự vẽ nha
kẻ OH vuông góc với CD
Kẻ OK là trung tuyến của tam giác CMD
xét tam giác CMD vuông tại M có
MK=CK = 1/2 CD (MK là tiếp tuyến )
=> CKM là tam giác cân, cân tại K
=> góc MKC = góc KMC
AC vuông góc với AB
BD vuông góc với AB
=> AC // BD
=>ACBD là hình thang
AM = MB
CK=KD
=>MK là đường trung bình
=> MK // CA
=> góc ACM = góc KMC
mà góc KMC = góc KCM (cmt)
=> góc ACM = góc KCM
=> góc HMC= góc CMA (cùng phụ 2 góc đó)
xét tam giác MAC và tam giác MHC có:
góc CAM = góc CHM = 90 độ
góc ACM= góc HCM ( cmt)
=> góc HMC= góc CMA
=> tam giác MAC = tam giác MHC
=> HM = AM mà HM vuông CD => ĐPCM
bài có ít sai sót ông xem thử nha