Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo.
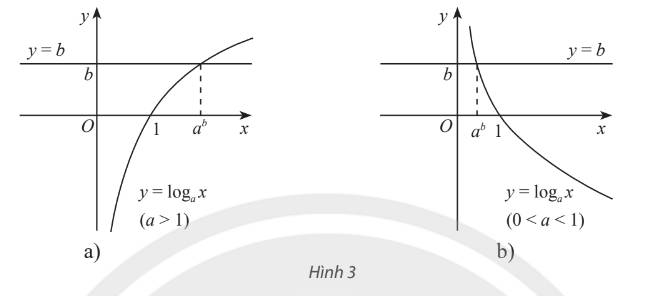
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\) có nghiệm duy nhất \(x=a^b\).

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
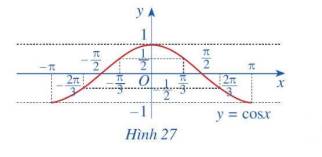
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
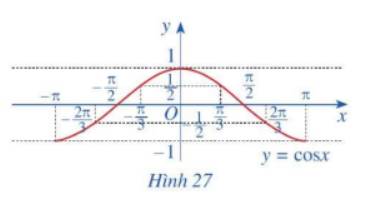
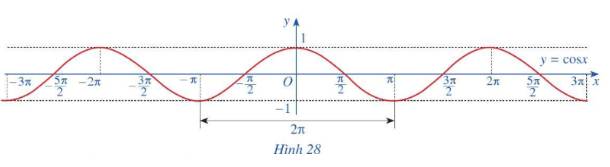
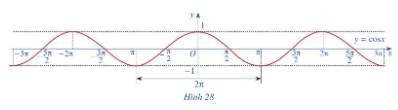
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

Ta có bảng sau:

Ta có đồ thị sau:
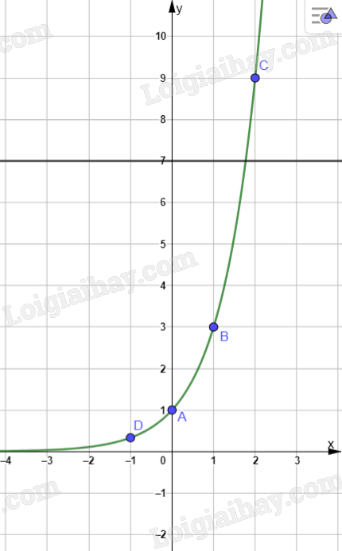
b, Hai đồ thị \(y=3^x\) và \(y=7\) có \(1\) giao điểm. Vậy số nghiệm của phương trình \(3^x=7\) là \(1\)

a:
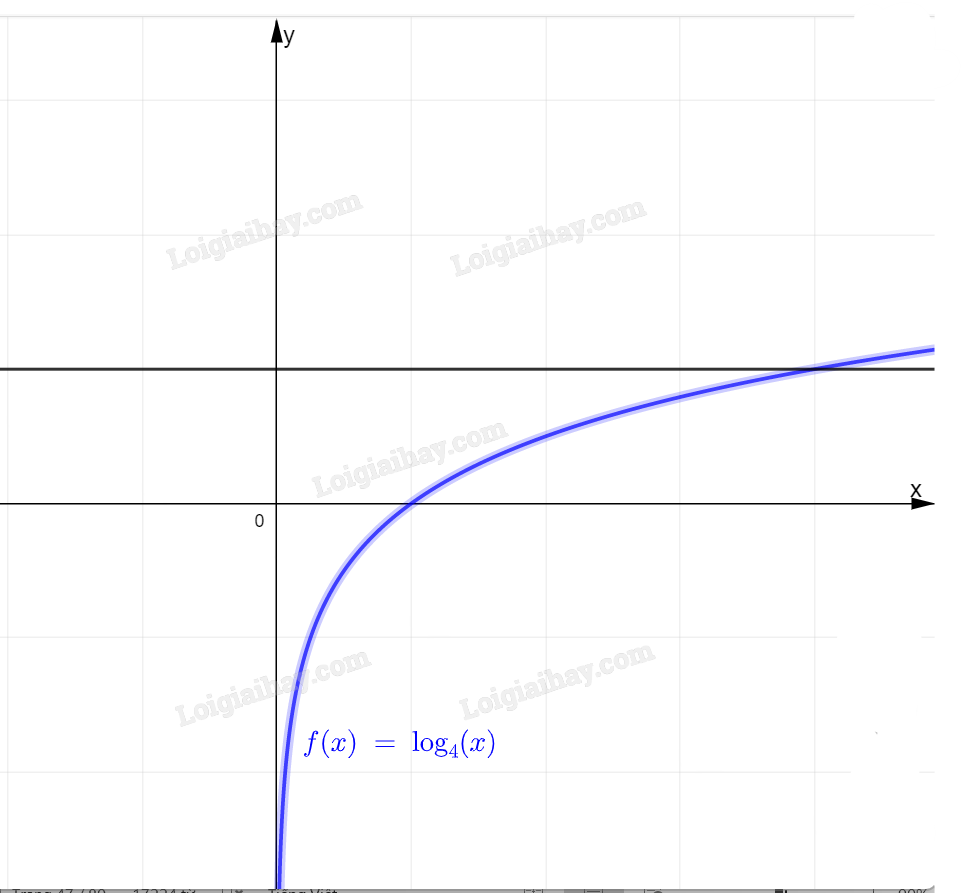
b: Hai đồ thị này có 1 giao điểm
=>Phương trình \(log_4x=5\) có 1 nghiệm duy nhất

a) Từ Hình 1.25, ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\;\)tại 1 điểm \(x = - \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = - \frac{\pi }{4} + \pi + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Xét phương trình tiếp tuyến tổng quát có dạng:
\(y=\left(6x_0+3x_0^2\right)\left(x-x_0\right)+3x_0^2+x_0^3\)
có 3 tiếp tuyến đi qua A(a,0) nên phương trình \(\left(6x_0+3x_0^2\right)\left(a-x_0\right)+3x_0^2+x_0^3=0\) có 3 nghiệm
\(PT\Leftrightarrow\orbr{\begin{cases}x_0=0\\2x_0^2+3\left(1-a\right)x_0+6a=0\end{cases}}\)
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì \(2x_0^2+3\left(1-a\right)x_0+6a=0\) có hia nghiệm \(x_1,x_2\text{ thỏa mãn}\)
\(\left(6x_1+3x_1^2\right)\left(6x_2+3x_2^2\right)=-1\)mà áp dung Viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{3a-3}{2}\\x_1x_2=3a\end{cases}}\)
Nên \(36x_1x_2+18x_1x_2\left(x_1+x_2\right)+9x_1^2x_2^2=-1\Leftrightarrow126a+81a\left(a-1\right)+81a^2=-1\)
từ đây mình giải được a nhé
Xét phương trình tiếp tuyến tổng quát có dạng:
y=(6x0+3x02)(x−x0)+3x02+x03
có 3 tiếp tuyến đi qua A(a,0) nên phương trình (6x0+3x02)(a−x0)+3x02+x03=0 có 3 nghiệm
PT⇔[
| x0=0 |
| 2x02+3(1−a)x0+6a=0 |
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì 2x02+3(1−a)x0+6a=0 có hia nghiệm x1,x2 thỏa mãn
(6x1+3x12)(6x2+3x22)=−1mà áp dung Viet ta có {
| x1+x2=3a−32 |
| x1x2=3a |
Nên 36x1x2+18x1x2(x1+x2)+9x12x22=−1⇔126a+81a(a−1)+81a2=−1

a)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).

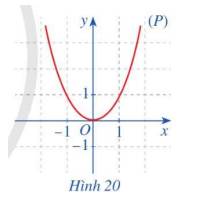
a)
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
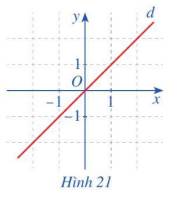
b)
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d
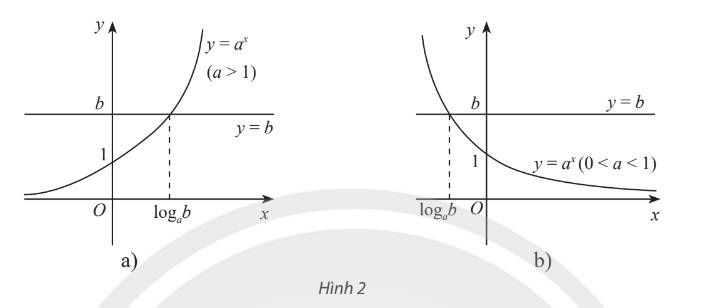





Khi \(b > 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) cắt nhau tại một điểm duy nhất. Khi đó phương trình \({a^x} = b\) có nghiệm duy nhất \(x = {\log _a}b\).
Khi \(b \le 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) không có điểm chung. Khi đó phương trình \({a^x} = b\) vô nghiệm.